৮ম শ্রেণি গণিত – Math class eight ১ম অধ্যায়: প্যাটার্ন
প্যাটার্ন, class 8 math pdf download, অষ্টম শ্রেণির গণিত সমাধানঃ অধ্যায়ঃ ১ প্যাটার্ন, ক্লাস 8 গণিত অধ্যায় 1, প্যাটার্ন এর সূত্র, ২, ৫, ৮, ১১, ১৪ …………… প্যাটার্নের ১০ম পদ কত?, অষ্টম শ্রেণির প্রথম অধ্যায়, প্যাটার্ন এর উদাহরণ, প্যাটার্ন এর সূত্র, প্যাটার্ন কাকে বলে class 8, জ্যামিতিক প্যাটার্ন কাকে বলে?
প্যাটার্ন: কোনো কিছুর নমুনা বা মডেলকেই প্যাটার্ন বলে । প্যাটার্ন এমনভাবে তৈরি করা হয়, যাতে আর্দ্র বালিতে ছাঁচ তৈরী করে গলানো ধাতু ঢালাই করে বস্তু বা জিনিস তৈরী করা যায়। নিম্ন-লিখিত 10 ( দশ) রকমের প্যাটার্ন আছে। সেগুলো নিচে দেওয়া হলো:
১। সিঙ্গল (single) পিচ প্যাটার্ন
২। গেটের প্যাটার্ন
৩। লুজ পিস প্যাটার্ন
৪। স্প্লিট প্যাটার্ন
৫। ম্যাচ প্লেট প্যাটার্ন
৬। কোপ অ্যান্ড ড্রাগ প্যাটার্ন
৭। সুইপ প্যাটার্ন
৮। লেফ্ট অ্যান্ড রাইট হ্যান্ড প্যাটার্ন
৯। শেল প্যাটার্ন ও
১০। বিল্ট আপ প্যাটার্ন।
জ্যামিতিক প্যাটার্ন: জ্যামিতিক অঙ্ক বা সংখ্যা দ্বারা গঠিত নকশা বা ডিজাইনকে জ্যামিতিক প্যাটার্ন বলে ।
অথবা. জ্যামিতিক চিত্রগুলো যে নমুনা তৈরি করে তাকে জ্যামিতিক প্যাটার্ন বলে।
অথবা, নিদিষ্ট পন্থায় কোন কিছু(সংখ্যা, নশকা বা চিত্র) সাজানোকে প্যাটার্ন বলে
অথবা, নিদিষ্ট পন্থায় কোন কিছু বানানোকে প্যাটার্ন বলে।
অনুশীলনী সমাধান
১। প্রতিটি তালিকার পরবর্তী চারটি সংখ্যা নির্নয় করঃ
(ক) ১, ৩, ৫, ৭, ৯, … (খ) ৪, ৮, ১২, ১৬, ২০, …
(গ) ৫, ১০, ১৫, ২০, ২৫, … (ঘ) ৭, ১৪, ২১, ২৮, ৩৫, …
(ঙ) ৮, ১৬, ২৪, ৩২, ৪০, … (চ) ৬, ১২, ১৮, ২৪, ৩০, …
(ক) ১, ৩, ৫, ৭, ৯, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ১, ৩, ৫, ৭, ৯, …
পার্থক্যঃ ৩-১=২, ৫-৩=২, ৭-৫=২, ৯-৭=২
অর্থাৎ প্রতিবার পার্থক্য হল ২।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
৯ + ২ = ১১
১১ + ২ = ১৩
১৩ + ২ = ১৫
১৫ + ২ = ১৭
উত্তরঃ১১,১৩,১৫,১৭
(খ) ৪, ৮, ১২, ১৬, ২০, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ৪, ৮, ১২, ১৬, ২০, …
পার্থক্যঃ ৮ – ৪ = ৪, ১২-৮ = ৪, ১৬-১২ = ৪, ২০-১৬ = ৪
অর্থাৎ প্রতিবার পার্থক্য হল ৪।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
২০ + ৪ = ২৪
২৪ + ৪ = ২৮
২৮ + ৪ = ৩২
৩২ + ৪ = ৩৬
উত্তরঃ ২৪,২৮,৩২,৩৬
(গ) ৫, ১০, ১৫, ২০, ২৫, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ৫, ১০, ১৫, ২০, ২৫, …
পার্থক্যঃ ১০ – ৫ = ৫, ১৫ – ১০ = ৫, ২০ – ১৫ = ৫, ২৫- ২০ = ৫
অর্থাৎ প্রতিবার পার্থক্য হল ৫।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
২৫ + ৫ = ৩০
৩০ + ৫ = ৩৫
৩৫ + ৫ = ৪০
৪০ + ৫ = ৪৫
উত্তরঃ ৩০,৩৫,৪০,৪৫
(ঘ) ৭, ১৪, ২১, ২৮, ৩৫, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ৭, ১৪, ২১, ২৮, ৩৫, …
পার্থক্যঃ ১৪-৭=৭, ২১-১৪ = ৭, ২৮-১৪ = ৭, ৩৪ – ২৮=৭
অর্থাৎ প্রতিবার পার্থক্য হল ৭।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
৩৫ + ৭ = ৪২
৪২ + ৭ = ৪৯
৪৯ + ৭ = ৫৬
৫৬ + ৭ = ৬৩
উত্তরঃ ৪২,৪৯,৫৬,৬৩
(ঙ) ৮, ১৬, ২৪, ৩২, ৪০, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ৮, ১৬, ২৪, ৩২, ৪০, …
পার্থক্যঃ ১৬-৮=৮,২৪-১৬=৮,৩২-২৪=৮,৪০-৩২=৮
অর্থাৎ প্রতিবার পার্থক্য হল ৮।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
৪০ + ৮ = ৪৮
৪৮ + ৮ = ৫৬
৫৬ + ৮ = ৬৪
৬৪ + ৮ = ৭২
উত্তরঃ ৪৮,৫৬,৬৪,৭২
(চ) ৬, ১২, ১৮, ২৪, ৩০, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ৬, ১২, ১৮, ২৪, ৩০, …
পার্থক্যঃ ১২-৬=৬,১৮-১২=৬,২৪-১৮=৬,৩০-২৪=৬
অর্থাৎ প্রতিবার পার্থক্য হল ৬।
অতএব, পরবর্তী চারটি সংখ্যা হবেঃ
৩০ + ৬ = ৩৬
৩৬ + ৬ = ৪২
৪২ + ৬ = ৪৮
৪৮ + ৬ = ৫৪
উত্তরঃ ৩৬,৪২,৪৮,৫৪
২। প্রতিটি তালিকার পাশাপাশি দুইটি পদের পার্থক্য বের কর ও পরব দুইটি সংখ্যা নির্নয় করঃ
(ক) ৭, ১২, ১৭, ২২, ২৭, …
(খ) ৬, ১৭, ২৮, ৩৯, ৫০, …
(গ) ২৪, ২০, ১৬, ১২, ৮, …
(ঙ) – ৫, – ৮, – ১১, – ১৪, …
(চ) ১৪, ৯, ৪, – ১, –৬, …
(ঘ) ১১, ৮, ৫, ২, – ১, …
(ক) ৭, ১২, ১৭, ২২, ২৭, …
সমাধান :
তালিকার সংখ্যা সমুহঃ৭, ১২, ১৭, ২২, ২৭, …
পার্থক্যঃ ১৭-১২=৫, ২২-১৭=৫, ২৭-২২=৫
অর্থাৎ প্রতিবার পার্থক্য হল ৫।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
২৭ + ৫ = ৩২
এবং ৩২ + ৫ = ৩৭ ।
উত্তরঃ ৩২,৩৭
(খ) ৬, ১৭, ২৮, ৩৯, ৫০, …
সমাধান :
তালিকার সংখ্যা সমুহঃ৬, ১৭, ২৮, ৩৯, ৫০, …
পার্থক্যঃ১৭-৬=১১, ২৮-১৭=১১, ৩৯-২৮=১১, ৫০-৩৯=১১
অর্থাৎ প্রতিবার পার্থক্য হল ১১।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
৫০ + ১১ = ৬১
এবং ৬১ + ১১ = ৭২।
উত্তরঃ ৬১,৭২
(গ) ২৪, ২০, ১৬, ১২, ৮, …
সমাধান :
তালিকার সংখ্যা সমুহঃ২৪, ২০, ১৬, ১২, ৮, …
পার্থক্যঃ ২৪-২০=৪, ২০-১৬=৪, ১৬-১২=৪, ১২-৮=৪
অর্থাৎ প্রতিবার পার্থক্য হলঃ ৪।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
৮ – ৪ = ৪
এবং ৪ – ৪ = ০।
উত্তরঃ ৪,০
(ঘ) ১১, ৮, ৫, ২, – ১, …
সমাধান :
তালিকার সংখ্যা সমুহঃ১১, ৮, ৫, ২, – ১, …
পার্থক্যঃ ১১-৮=৩, ৮-৫=৩, ২+১=৩ {২- -১=২+১=৩}
অর্থাৎ প্রতিবার পার্থক্য হলঃ ৩।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
– ১ – ৩ = – ৪
এবং – ৪ – ৩ = – ৭।
উউরঃ -৪,-৭।
(ঙ) – ৫, – ৮, – ১১, – ১৪, …
সমাধান :
তালিকার সংখ্যা সমুহঃ– ৫, – ৮, – ১১, – ১৪, …
পার্থক্যঃ -৮+৫=-৩, -১১+৮=-৩, -১৪+১১=-৩
অর্থাৎ প্রতিবার পার্থক্য হল – ৩।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
– ১৪ – ৩ = – ১৭
এবং – ১৭ – ৩ = – ২০।
উত্তরঃ -১৭, -২০
(চ) ১৪, ৯, ৪, – ১, –৬, …
সমাধান :
তালিকার সংখ্যা সমুহঃ ১৪, ৯, ৪, – ১, –৬, …
পার্থক্যঃ ১৪-৯=৫, ৪+১=৫, -১+৬=৫
অর্থাৎ প্রতিবার পার্থক্য হল ৫।
অতএব, পরবর্তী দুইটি সংখ্যা হবেঃ
– ৬ – ৫ = – ১১
এবং – ১১ – ৫ = – ১৬
উত্তরঃ -১১, -১৬।
৩। তালিকার পরবর্তি দুইটি সংখ্যা নির্নয় কর :
(ক) ২, ২, ৪, ৮, ১৪, ২২, … (খ) ০, ৩, ৮, ১৫, ২৪, …
(গ) ১, ৪, ১০, ২২, ৪৬, … (ঘ) ৪, – ১, – ১১, – ২৬, – ৪৬, …
(ক) ২, ২, ৪, ৮, ১৪, ২২, …
সমাধান :
প্রদত্য তালিকাঃ ২, ২, ৪, ৮, ১৪, ২২, …
পার্থক্যঃ ০ ২ ৪ ৬ ৮
প্রতিবার পার্থক্য ২ এর গুনিতক হারে বেড়েছে।
এ অনুযায়ী পরবর্তী দুটি পার্থক্য হবেঃ (৮+২) = ১০ ও (১০+২) = ১২
অতএব পরবর্তি দুটি সংখ্যাঃ ২২ + ১০ = ৩২ এবং ৩২ + ১২ = ৪৪
উত্তরঃ ৩২, ৪৪।
(খ) ০, ৩, ৮, ১৫, ২৪, …
সমাধান :
প্রদত্য তালিকাঃ ০, ৩, ৮, ১৫, ২৪, …
পার্থক্যঃ৩ ৫ ৭ ৯
প্রতিবার পার্থক্য ২ করে বেড়েছে।
অতএব পরবর্তি দুটি সংখ্যাঃ ২৪ + ১১ = ৩৫ এবং ৩৫ + ১৩ = ৪৮
উত্তরঃ ৩৫, ৪৮।
(গ) ১, ৪, ১০, ২২, ৪৬, …
সমাধান :
প্রদত্য তালিকাঃ ১, ৪, ১০, ২২, ৪৬, …
পার্থক্যঃ৩ ৬ ১২ ২৪
প্রতিবার পার্থক্য ২ এর গুনিতক হারে বেড়েছে।
এ অনুযায়ী পরবর্তী দুটি পার্থক্য হবেঃ ৪৮ ও ৯৬
অতএব পরবর্তি দুটি সংখ্যাঃ ৪৬ + ৪৮ = ৯৪ এবং ৯৪ + ৯৬ = ১৯০
উত্তরঃ ৯৪ ও ১৯০।
(ঘ) ৪, – ১, – ১১, – ২৬, – ৪৬, …
সমাধান :
প্রদত্য তালিকাঃ ৪, – ১, – ১১, – ২৬, – ৪৬, …
পার্থক্যঃ– ৫ – ১০ – ১৫ – ২০
প্রতিবার পার্থক্য ৫ এর গুনিতক হারে কমেছে।
অতএব পরবর্তি দুটি সংখ্যাঃ – ৪৬ – ২৫ = – ৭১ এবং – ৭১ – ৩০ = – ১০১
উত্তরঃ – ৭১ ও – ১০১।
৪। নিচের সংখ্যা প্যাটার্নগুলোর মধ্যে কোন মিল রয়েছে কি? প্রতিটি তালিকার পরের সংখ্যা বের কর?
(ক) ১, ১, ২, ৩, ৫, ৮, ১৩, … (খ) ৪, ৪, ৫, ৬, ৮, ১১, …
(গ) – ১, – ১, ০, ১, ৩, ৬, ১১, …
(ক) ১, ১, ২, ৩, ৫, ৮, ১৩, …
সমাধান :
প্রদত্য তালিকাঃ ১, ১, ২, ৩, ৫, ৮, ১৩, …
পার্থক্যঃ ০ ১ ১ ২ ৩ ৫
মিলঃ প্যাটার্নটিতে প্রথম দুটি সংখ্যা একই, পার্থক্যের সিরিয়ালও প্যাটার্নের অনুরুপ এবং পর পর দুটি সংখ্যার যোগফল পরবর্তি সংখ্যার সমান, যেমন-১+২=৩।
অতএব তালিকার পরের সংখ্যাঃ ৮+১৩=২১।
(খ) ৪, ৪, ৫, ৬, ৮, ১১, …
সমাধান :
প্রদত্য তালিকাঃ ৪, ৪, ৫, ৬, ৮, ১১, …
পার্থক্যঃ ০ ১ ১ ২ ৩
মিলঃ প্যাটার্নটিতে প্রথম দুটি সংখ্যা একই, সংখ্যাগুলোর পার্থক্যের যে সিরিয়াল তাতে পরপর দুটি সংখ্যার যোগ তৃতীয় সংখ্যার সমান।
এই অনুযায়ি পরবর্তি পার্থক্যঃ ৩+২=৫
সুতরাং তালিকার পরের সংখ্যাঃ ১১+৫=১৬।
(গ) – ১, – ১, ০, ১, ৩, ৬, ১১, …
সমাধান :
প্রদত্য তালিকাঃ – ১, – ১, ০, ১, ৩, ৬, ১১, …
পার্থক্যঃ ০ ১ ১ ২ ৩ ৫
মিলঃ প্যাটার্নটিতে প্রথম দুটি সংখ্যা একই, সংখ্যাগুলোর পার্থক্যের যে সিরিয়াল তাতে পরপর দুটি সংখ্যার যোগ তৃতীয় সংখ্যার সমান।
এই অনুযায়ি পরবর্তি পার্থক্যঃ ৩+৫=৮
সুতরাং তালিকার পরের সংখ্যাঃ ১১ + ৮= ১৯
৫। কোন এক কম্পিউটার প্রোগ্রাম থেকে নিচের সংখ্যাগুলো পাওয়া গেল :
১ ২ ৪ ৮ ১১ ১৬ ২২
এ সংখ্যাগুলোর একটি সংখ্যা পরিবর্তন করা হলে সংখ্যাগুলো একটি প্যাটার্ন তৈরি করে। সংখ্যাটি চিহ্নিত করে উপযুক্ত সংখ্যাটি বসাও।
সমাধান :
প্রদত্য তালিকাঃ ১, ২, ৪, ৮, ১১, ১৬, ২২
পার্থ্যকঃ ১ ২ ৪ ৩ ৫ ৬
তালিকার সংখ্যাগুলোর পার্থক্য হেত দেখা যায়, ৩য় ও ৪র্থ পার্থক্যটি সঠিক নয়। ফলে তালিকাটি কোন প্যাটার্ন তৈরি করেনি। যদি সংখ্যাগুলোর পার্থক্য ৪ এর পরিবর্তে ৩ ও ৩ এর পরিবর্তে ৪ হয় তবে সংখ্যাগুলো একটি প্যাটার্ন তৈরি করে। তখন চতুর্থ সংখ্যা ৮ এর পরিবর্তে হবে ৪+৩=৭
অতএব, তালিকাটিঃ ১ ২ ৪ ১১ ১৬ ২২
পার্থ্যকঃ ১ ২ ৩ ৪ ৫ ৬
সুতরাং, উপযুক্ত সংখ্যা হল ৭।
৬। বীজগণিতীয় রাশির মাধ্যমে সংখ্যা পাটার্ন এর সারণিটি তৈরি কর?
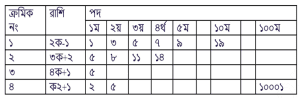
সমাধানঃ
নিচে বীজগণিতীয় রাশির মাধ্যমে সংখ্যা পাটার্ন এর সারণিটি তৈরি করা হল:

৭। নিচেরর জ্যামিতিক চিত্রগুলো কাঠি দিয়ে তৈরি করা হয়েছে।

(ক) কাঠির সংখ্যার তালিকা কত?
(খ) তালিকার পরবর্তি সংখ্যাটি কিভাবে বের করবে তা ব্যাখ্যা কর।
(গ) কাঠি দিয়ে পরবর্তি চিত্রটি তৈরি কর এবং তোমার উত্তর যাচাই কর।
সমাধান :
(ক) কাঠির সংখ্যার তালিকা: ৪, ৭, ১০
(খ)তালিকার পরবর্তি সংখ্যাঃ প্রাপ্ত তালিকাঃ ৪, ৭, ১০
পার্থক্যঃ ৩, ৩
প্রত্যেকবার পার্থক্যঃ ৩।
সুতরাং পরবর্তি সংখ্যাঃ ১০ + ৩ = ১৩
(গ) পরবর্তী চিত্র:

কাঠি দিয়ে তৈরি প্রদত্ত প্যাটার্ন থেকে দেখা যায় যে, প্রতি ক্ষেত্রে একটি আয়তাকার কলাম যোগ হচ্ছে। এটি এমনভাবে পূর্ববর্তী জ্যামিতিক চিত্রের সাথে যুক্ত হচ্ছে যাতে পূর্ববর্তী চিত্রের ডানদিকের কাঠিটি নতুন করে যুক্ত হওয়ায় চিত্রের বামদিকের কাঠি হিসেবে কাজ করে। অর্থাৎ প্রতিক্ষেত্রে আয়তাকৃতি কলাম বা জ্যামিতিক চিত্র তৈরিতে ৪টি কাঠির পরিবর্তে ৩টি কাঠি ব্যবহৃত হচ্ছে। সুতরাং প্রতিক্ষেত্রে ৩টি কাঠি যুক্ত করে পরবর্তি চিত্রটি তৈরি করা হয় বলে তৈরিকৃত জ্যামিতিক চিত্রটি যথাযথ। ।
৮। দিয়াশলাইয়রে কাঠি দিয়ে নিচের ত্রিভুজগুলোর প্যাটার্ন তৈরি করা হইয়েছে।

(ক) চতুর্থ প্যাটার্নে দিয়াশলাইয়ের কাঠির সংখ্যা বের কর।
(খ) তালিকার পরবর্তী সংখ্যাটি কীভাবে বের করবে তা ব্যাখ্যা কর।
(গ) শততম প্যাটার্ন তৈরিতে কতগুলো দিয়াশলাইয়ের কাঠির প্রয়োজন?
সমাধান :
(ক) চতুর্থ প্যাটার্নটি হলো :

চিত্র থেকে দেখা যায়, চতুর্থ প্যাটার্নে কাঠি সংখ্যা ৯ টি
(খ) প্রদত্ত তালিকার সংখ্যা: ৩, ৫, ৭
পার্থক্যঃ ২, ২
সুতরাং পরবর্তী সংখ্যাটি হবেঃ ৭ + ২ = ৯
(গ) প্রদত্ত তালিকার সংখ্যা: ৩, ৫, ৭
পার্থক্যঃ ২ ২
উক্ত প্যাটার্নের জন্য বীজগণিতীয় রাশিমালা = ২ক + ১
এখানে ‘ক হল প্যাটার্নের সংখ্যা।
সুতরাং শততম প্যাটার্ন তৈরিতে কতগুলো দিয়াশলাইয়ের কাঠির প্রয়োজন= ২ * ১০০ + ১= ২০১টি
সৃজনশীল প্রশ্ন:
১। ৪, ৭, ১০, ১৩, . . . . . . . . . . . . একটি সংখ্যা প্যাটার্ণ।
(ক) ৩২৫ কে তিনটি ভিন্ন উপায়ে দুইটি বর্গের সমষ্টিরূপে প্রকাশ কর।
(খ) তালিকাটির বীজগণিতীয় রাশি নির্ণয় কর।
(গ) তালিকাটির ১ম পদ বাদে অবশিষ্ট পদ নিয়ে গঠিত প্যাটার্ণের ১ম ১০টি পদের সমষ্টি বের
২। ১, ৪, ৯, ১৬, ২৫, . . . . . . . . . . একটি সংখ্যা প্যাটার্ণ।
(ক) স্বাভাবিক ক্রমিক সংখ্যার যোগফল নির্ণয়ের সূত্রটি লেখ।
(খ) তালিকার পরবর্তী তিনটি সংখ্যা নির্ণয় কর।
(গ) প্রথম থেকে ২০তম পার্থক্য পর্যন্ত পার্থক্যগুলোর সমষ্টি বের কর।
৩। ১, ১, ২, ৩, ৫, ৮, ১৩, . . . . . . . . . একটি প্যাটার্ন এবং ২ক +১ একটি বীজগণিতীয় রাশি।
(ক) ফিবোনাক্কি সংখ্যা কী? ব্যাখ্যা কর।
(খ) সংখ্যা প্যাটার্নটির পরবর্তী চারটি পদের মান নির্ণয় কর।
(গ) বীজগণিতীয় রাশিটির প্রথম ৫০টি পদের সমষ্টি নির্ণয় কর।
৪। ৫, ১৩, ২৪, ৩৮, ৫৫, . . . . . . . . . . একটি সংখ্যা প্যাটার্ন।
(ক) যেকোনো একটি কৌশলে ৪ ক্রমের একটি ম্যাজিক বর্গ গঠণ কর।
(খ) তালিকার পরবর্তী চারটি পদ নির্ণয় করে তাদের যোগফল বের কর।
(গ) তালিকার সংখ্যাগুলোর পার্থক্য যে প্যাটার্ন তৈরি করে তার যেকোনো পদ নির্ণয় করার একটি সাধারণ সূত্র তৈরি কর এবং প্রথম ৫০টি পদের সমষ্টি নির্ণয় কর।
৫। ৭, ১৬, ২৫, ৩৪, ৪৩, . . . . . . . . . . . একটি সংখ্যা প্যাটার্ন।
(ক) তৃতীয় ও চতুর্থ সংখ্যাকে দুইটি বর্গের সমষ্টিরূপে প্রকাশ কর।
(খ) তালিকার সাধারণ অন্তর এবং পরবর্তী তিনটি সংখ্যা নির্ণয় কর।
(গ) তালিকার ৪৫তম পদ এবং ১ম ৪৫টি পদের সমষ্টি নির্ণয় কর।
৬। ৫, ১৩, ২১, ২৯, ৩৭, . . . . . . . . . . . . . . .
(ক) ২৯ এবং ৩৭ কে দু’টি বর্গের সমষ্টিরূপে প্রকাশ কর।
(খ) তালিকার পরবর্তী ৪টি সংখ্যা নির্ণয় কর।
(গ) তালিকার প্রথম ৫০টি সংখ্যার সমষ্টি নির্ণয় কর।
৭। ৭, ১১, ১৫, ১৯, ২৩, ২৭, . . . . . . . . . . . একটি সংখ্যা প্যাটার্ন।
(ক) ৪০ কে দুইটি বর্গের অন্তর এবং ১০০ কে দুইটি বর্গের সমষ্টিরূপে প্রকাশ কর।
(খ) উদ্দীপকে প্রদত্ত সংখ্যাগুলো কোন নিয়মে প্যাটার্নভূক্ত হলো তা দেখাও এবং যেকোনো পদ নির্ণয়ের সূত্র ’ক’ চলকের সাহায্যে প্রকাশ কর।
(গ) প্যাটার্নটির প্রথম ২৫টি পদের সমষ্টি নির্ণয় কর।
৮। (৫ক+৭) একটি বীজগাণিতিক রাশি, যেখানে ‘ক’ একটি স্বাভাবিক সংখ্যা।
(ক) রাশিটির ১ম ও ২য় পদ নির্ণয় কর।
(খ) উদ্দীপকের আলোকে ১ম তিনটি পদের জ্যামিতিক প্যাটার্ন অঙ্কন করে মোট রেখাংশের সংখ্যা নির্ণয় কর।
(গ) রাশিটির প্রথম পঞ্চাশটি পদের সমষ্টি সূত্রের সাহায্যে নির্ণয় কর।
৯। ৩ক+১ কোনো সংখ্যা তালিকার বীজগণিতীয় রাশি।
(ক) ৩২৫ কে দুইটি ভিন্ন উপায়ে দুইটি বর্গের সমষ্টিরূপে প্রকাশ কর।
(খ) উদ্দীপকের আলোকে ৩য় ও ৪র্থ পদের জ্যামিতিক প্যাটার্ন অঙ্কন কর এবং অঙ্কনের সত্যতা যাচাই কর।
(গ) রাশিটির প্রথম ১০০ পদের সমষ্টি নির্ণয় কর।
১০। (৫ক +২) একটি বীজগণিতীয় রাশি।
(ক) রাশিটির ১ম ও ২য় পদ কত?
(খ) উদ্দীপকের আলোকে ৩য় ও ৪র্থ পদের জ্যামিতিক প্যাটার্ন অঙ্কন কর এবং অঙ্কনের সত্যতা যাচাই কর।
(গ) রাশিটির প্রথম ১০০ পদের সমষ্টি নির্ণয় কর।
