SSC math chapter 1- real numbers solution || বাস্তব সংখ্যা
স্বাভাবিক সংখ্যা (Natural Number) : 1, 2, 3, 4, …………… ইত্যাদি সংখ্যাগুলোকে স্বাভাবিক সংখ্যা বা ধনাত্মক অখণ্ড সংখ্যা বলে। 2, 3, 5, 7, …………… ইত্যাদি মৌলিক সংখ্যা এবং 4, 6, 8, 9, …………… ইত্যাদি যৌগিক সংখ্যা।
পূর্ণসংখ্যা (Integer) : শূন্যসহ সকল ধনাত্মক ও ঋণাত্মক অখণ্ড সংখ্যাসমূহকে পূর্ণসংখ্যা বলা হয়।
অর্থাৎ …………… -3, – 2, – 1, 0, 1, 2, 3, ……………ইত্যাদি পূর্ণসংখ্যা।
ভগ্নাংশ সংখ্যা (Fractional Number) : p, q পরস্পর সহমৌলিক, p ≠ 0, এবং q ≠ 1 হলে, \[\frac{p}{q}\] আকারের সংখ্যাকে ভগ্নাংশ সংখ্যা বলে। যেমন : \[\frac{1}{2}\], \[\frac{3}{2}\], \[ -\frac{1}{2}\] ইত্যাদি ভগ্নাংশ সংখ্যা।
p < q হলে ভগ্নাংশকে প্রকৃত ভগ্নাংশ এবং p > q হলে ভগ্নাংশকে অপ্রকৃত ভগ্নাংশ বলা হয়।
যেমন : \[ \frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{1}{4} \] ……………. ইত্যাদি প্রকৃত ভগ্নাংশ এবং \[ \frac{3}{2}, \frac{4}{3}, \frac{5}{3}, \frac{5}{4} \] ইত্যাদি অপ্রকৃত ভগ্নাংশ।
মূলদ সংখ্যা (Rational Number) : p ও q পূর্ণসংখ্যা এবং q ≠ 0 হলে, \[\frac{p}{q}\] আকারের সংখ্যাকে মূলদ সংখ্যা বলা হয়।
যেমন : \[ \frac{3}{1} = 3, \frac{11}{2} = 5.5, \frac{5}{3} = 1.6666……. \] ইত্যাদি মূলদ সংখ্যা।
অমূলদ সংখ্যা (Irrational Number) : যে সংখ্যাকে\[\frac{p}{q}\] আকারে প্রকাশ করা যায় না, যেখানে p, q পূর্ণসংখ্যা এবং q ≠ 0, সে সংখ্যাকে অমূলদ সংখ্যা বলা হয়। পূর্ণবর্গ নয় এরূপ যেকোনো স্বাভাবিক সংখ্যার বর্গমূল একটি অমূলদ সংখ্যা।
যেমন : \[\sqrt{2} = 1.414213 ……., \sqrt{3} = 1.732 ……., \frac{\sqrt{5}}{2} = 1.58113 …….. \] ইত্যাদি অমূলদ সংখ্যা। অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসাবে প্রকাশ করা যায় না।
দশমিক ভগ্নাংশ সংখ্যা : মূলদ সংখ্যা ও অমূলদ সংখ্যাকে দশমিকে প্রকাশ করা হলে একে দশমিক ভগ্নাংশ বলা হয়।
যেমন : \[ 3 = 3.0 , \frac{5}{2} = 2.5, \frac{10}{3} = 3.33333 ….., \sqrt{3} = 1.732 ……. \] ইত্যাদি দশমিক ভগ্নাংশ সংখ্যা।
বাস্তব সংখ্যা (Real Number) : সকল মূলদ সংখ্যা এবং অমূলদ সংখ্যাকে বাস্তব সংখ্যা বলা হয়।
ধনাত্মক সংখ্যা (Positive Number) : শূন্য অপেক্ষা বড় সকল বাস্তব সংখ্যাকে ধনাত্মক সংখ্যা বলা হয়।
যেমন : \[ 1, 2 , \frac{1}{2}, \frac{3}{2}, \sqrt{2} , \overset.62, 0.415, 4.120345061, ……. \] ইত্যাদি ধনাত্মক সংখ্যা।
ঋণাত্মক সংখ্যা (Negative Number) : শূন্য অপেক্ষা ছোট সকল বাস্তব সংখ্যাকে ঋণাত্মক সংখ্যা বলা হয়।
যেমন : \[ -1, – 2 , – \frac{1}{2}, – \frac{3}{2}, – \sqrt{2} , – \overset.62, – 0.415, – 4.120345061, ……. \] ইত্যাদি ঋণাত্মক সংখ্যা।
অঋণাত্মক সংখ্যা (Non-negative Number) : শূন্যসহ সকল ধনাত্মক সংখ্যাকে অঋণাত্মক সংখ্যা বলা হয়।
যেমন : \[ 0 , 2 , \frac{1}{2}, \frac{3}{2}, , \overset.62, 0.415, 4.120345061, ……. \] ইত্যাদি অঋণাত্মক সংখ্যা।
অনুশীলনী সমাধান
প্রশ্ন \ ১ \ প্রমাণ কর যে, (ক) \[\sqrt{5}\] (খ) \[\sqrt{7}\] (গ) \[\sqrt{10}\] প্রত্যেকে অমূলদ সংখ্যা
সমাধান : (ক) এখানে, 22 = 4; 32 = 9 এবং \[(\sqrt{5})^2\] = 5
সুতরাং \[\sqrt{5}\] , 2 অপেক্ষা বড় কিন্তু 3 অপেক্ষা ছোট সংখ্যা।
অতএব, \[\sqrt{5}\] পূর্ণসংখ্যা নয়। অর্থাৎ \[\sqrt{5}\] মূলদ বা অমূলদ সংখ্যা।
মনে করি, \[\sqrt{5}\] মূলদ সংখ্যা।
তাহলে ধরি, \[\sqrt{5} = \frac{p}{q}\] ; যেখানে p ও q স্বাভাবিক সংখ্যা, q ≠ 0 এবং p, q সহমৌলিক, q >1.
বা, 5 = \[ \frac{p^2}{q^2}\]; বর্গ করে
বা, 5q = \[ \frac{p^2}{q}\] ; উভয় পক্ষকে q দ্বারা গুণ করে।
এখানে, 5q স্পষ্টত পূর্ণসংখ্যা কিন্তু \[ \frac{p^2}{q}\] পূর্ণসংখ্যা নয়। কারণ p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q > 1.
সুতরাং, 5q এবং \[ \frac{p^2}{q}\] সমান হতে পারে না, অর্থাৎ 5q ≠ \[ \frac{p^2}{q}\]
\[\sqrt{5}\] এর মান \[ \frac{p}{q}\] আকারের কোনো সংখ্যা হতে পারে না,
অর্থাৎ, \[\sqrt{5}\] ≠ \[ \frac{p}{q}\]
অতএব, \[\sqrt{5}\] একটি অমূলদ সংখ্যা। (প্রমাণিত)
(খ) এখানে, 4 < 7 < 9
বা, \[\sqrt{4} < \sqrt{7} < \sqrt{9} \]
বা, \[2 < \sqrt{7} < 3 \]
∴ \[\sqrt{7}\] , 2 অপেক্ষা বড় কিন্তু 3 অপেক্ষা ছোট সংখ্যা
অতএব, \[\sqrt{7}\] পূর্ণসংখ্যা নয়, অর্থাৎ \[\sqrt{7}\] মূলদ বা অমূলদ সংখ্যা
মনে করি, \[\sqrt{7}\] মূলদ সংখ্যা।
তাহলে ধরি, \[\sqrt{7} = \frac{p}{q}\] ; যেখানে p ও q স্বাভাবিক সংখ্যা, q ≠ 0 এবং p, q সহমৌলিক, q >1.
বা, 7 = \[ \frac{p^2}{q^2}\]; বর্গ করে
বা, 7q = \[ \frac{p^2}{q}\] ; উভয় পক্ষকে q দ্বারা গুণ করে।
এখানে, 7q স্পষ্টত পূর্ণসংখ্যা কিন্তু \[ \frac{p^2}{q}\] পূর্ণসংখ্যা নয়। কারণ p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q > 1.
সুতরাং, 7q এবং \[ \frac{p^2}{q}\] সমান হতে পারে না, অর্থাৎ 7q ≠ \[ \frac{p^2}{q}\]
\[\sqrt{7}\] এর মান \[ \frac{p}{q}\] আকারের কোনো সংখ্যা হতে পারে না,
অর্থাৎ, \[\sqrt{7}\] ≠ \[ \frac{p}{q}\]
অতএব, \[\sqrt{7}\] একটি অমূলদ সংখ্যা। (প্রমাণিত)
(গ) এখানে, , 9 < 10 < 16
বা, \[\sqrt{9} < \sqrt{10} < \sqrt{16} \]
বা, \[ 3 < \sqrt{10} < 4 \]
∴ \[\sqrt{10}\] পূর্ণ সংখ্যা নয়, অর্থাৎ \[\sqrt{10}\] মূলদ বা অমূলদ সংখ্যা
মনে করি, \[\sqrt{10}\] মূলদ সংখ্যা।
তাহলে ধরি, \[\sqrt{10} = \frac{p}{q}\] ; যেখানে p ও q স্বাভাবিক সংখ্যা, q ≠ 0 এবং p, q সহমৌলিক, q >1.
বা, 10 = \[ \frac{p^2}{q^2}\]; বর্গ করে
বা, 10q = \[ \frac{p^2}{q}\] ; উভয় পক্ষকে q দ্বারা গুণ করে।
এখানে, 10q স্পষ্টত পূর্ণসংখ্যা কিন্তু \[ \frac{p^2}{q}\] পূর্ণসংখ্যা নয়। কারণ p ও q স্বাভাবিক সংখ্যা ও এরা পরস্পর সহমৌলিক এবং q > 1.
সুতরাং, 10q এবং \[ \frac{p^2}{q}\] সমান হতে পারে না, অর্থাৎ 10q ≠ \[ \frac{p^2}{q}\]
\[\sqrt{10}\] এর মান \[ \frac{p}{q}\] আকারের কোনো সংখ্যা হতে পারে না,
অর্থাৎ, \[\sqrt{10}\] ≠ \[ \frac{p}{q}\]
অতএব, \[\sqrt{10}\] একটি অমূলদ সংখ্যা। (প্রমাণিত)
২। (ক) 0.31 এবং 0.12 এর মধ্যে দুইটি অমূলদ সংখ্যা নির্ণয় কর।
সমাধান : মনে করি, একটি সংখ্যা, a = 0.30300300030……………..
এবং অপর সংখ্যা, b = 0.2020020002……………..
স্পষ্টত : a ও b উভয়ই দুইটি বাস্তব সংখ্যা এবং উভয়ই 0.31 অপেক্ষা ছোট এবং 0.12 অপেক্ষা বড়
অর্থাৎ, 0.31 > 0.3030030003…………… > 0.12
এবং 0.31 > 0.2020020002…………… > 0.12
আবার, a ও b কে ভগ্নাংশ আকারে প্রকাশ করা যায় না।
∴ a ও b দুইটি নির্ণেয় অমূলদ সংখ্যা, যা 0.31 এবং 0.12 এর মাঝে অবস্থিত।
নির্ণেয় সংখ্যা, 0.3030030003……………
এবং 0.31 > 0.2020020002…………… > 0.12
[ বি. দ্র. : এরূপ অসংখ্য অমূলদ সংখ্যা নির্ণয় করা যায়।]
(খ) \[\frac{1}{\sqrt{2}}\] এবং \[ \sqrt{2}\] এর মধ্যে একটি মূলদ এবং একটি অমূলদ সংখ্যা নির্ণয় কর।
সমাধান : ক্যালকুলেটর ব্যবহার করে পাই,
\[\frac{1}{\sqrt{2}}\] = 0.7071 এবং \[ \sqrt{2}\] = 1.4142
মনে করি, একটি সংখ্যা a = \[\frac{7}{5}\] = 1.4
এবং অপর সংখ্যা b = 1.404004000400004………….
স্পষ্টত : a ও b উভয়ই বাস্তব সংখ্যা এবং উভয়ই \[\frac{1}{\sqrt{2}}\] অপেক্ষা বড় এবং \[ \sqrt{2}\] অপেক্ষা ছোট।
অর্থাৎ, 0×7071 < 1×4 ……………. < 1×4142
এবং 0×7071 < 1×404004000400004………….. < 1×4142
আবার, a কে ভগ্নাংশ আকারে প্রকাশ করা যায় ও b কে ভগ্নাংশ আকারে প্রকাশ করা যায় না।
এখন, \[\frac{7}{5}\] ও 1.4142 এর মাঝে a ও b অবস্থিত এবং a মূলদ সংখ্যা ও b অমূলদ সংখ্যা।
শর্তমতে, a মূলদ সংখ্যা ও b অমূলদ সংখ্যা যা 0.7071 এবং 1.4142 এর মাঝে অবস্থিত।
নির্ণেয় মূলদ সংখ্যা, \[\frac{7}{5}\] বা, 1.4
এবং অমূলদ সংখ্যা 1.404004000400004 ……………..
[ বি. দ্র. : এরূপ অসংখ্য মূলদ ও অমূলদ সংখ্যা নির্ণয় করা যায়।]
প্রশ্ন \ ৩ \ (ক) প্রমাণ কর যে, যেকোনো বিজোড় পূর্ণ সংখ্যার বর্গ একটি বিজোড় সংখ্যা।
সমাধান : মনে করি, n একটি বিজোড় সংখ্যা
∴ n = 2x – 1; যেখানে ী একটি পূর্ণ সংখ্যা
∴ n2 = (2x -1)2; উভয়পক্ষকে বর্গ করে
= (2x)2 – 2×2x×1 + (1)2
= 4x2 – 4x + 1 = 4x(x -1) + 1
এখানে, 4x(x -1) সংখ্যাটি 2 দ্বারা বিভাজ্য। অর্থাৎ জোড় সংখ্যা।
∴ 4x(x -1) + 1 সংখ্যাটি বিজোড় সংখ্যা।
অতএব, n2 বিজোড় সংখ্যা।
সুতরাং সকল বিজোড় পূর্ণ সংখ্যার বর্গ একটি বিজোড় সংখ্যা (প্রমাণিত)
(খ) প্রমাণ কর যে, দুইটি ক্রমিক জোড় সংখ্যার গুণফল 8 (আট) দ্বারা বিভাজ্য।
সমাধান : মনে করি, দুইটি ক্রমিক জোড় সংখ্যা যথাক্রমে 2x ও 2x + 2
ক্রমিক সংখ্যা দুইটির গুণফল, 2x ´ (2x + 2); যেখানে x যেকোনো স্বাভাবিক সংখ্যা।
∴ 2x ×(2x + 2) = 2x (2x + 2) = 4x2 + 4x = 4x (x + 1)
এখানে, x ও x + 1 দুইটি ক্রমিক সংখ্যা। সুতরাং এদের একটি জোড় সংখ্যা হবেই।
∴ x(x + 1) সংখ্যাটি 2 দ্বারা বিভাজ্য হবে।
∴ 4x(x +1) সংখ্যাটি 4 ´ 2 বা 8 দ্বারা বিভাজ্য হবে।
অতএব, দুইটি ক্রমিক জোড় সংখ্যার গুণফল 8 দ্বারা বিভাজ্য হবে।
সুতরাং x এর স্বাভাবিক মান নির্বিশেষে 8 দ্বারা 4x(x +1) সংখ্যাটি বিভাজ্য হবে। (প্রমাণিত)
প্রশ্ন \ ৪ \ আবৃত্ত দশমিক ভগ্নাংশে প্রকাশ কর :

লক্ষ করি, ভগ্নাংশের লবকে হর দিয়ে ভাগ করে দশমিক ভগ্নাংশে পরিণত করার সময় ভাগের প্রক্রিয়া শেষ হয় নাই। দেখা যায় যে, ভাগফলে একই সংখ্যা 6 বার বার আসে। এখানে 0×16666…………….একটি আবৃত্ত দশমিক ভগ্নাংশ।
নির্ণেয় আবৃত্ত দশমিক ভগ্নাংশ = 0.16666 …………..= \[ 0×1\overset.6 \]



প্রশ্ন \ ৫ \ সাধারণ ভগ্নাংশে প্রকাশ কর :
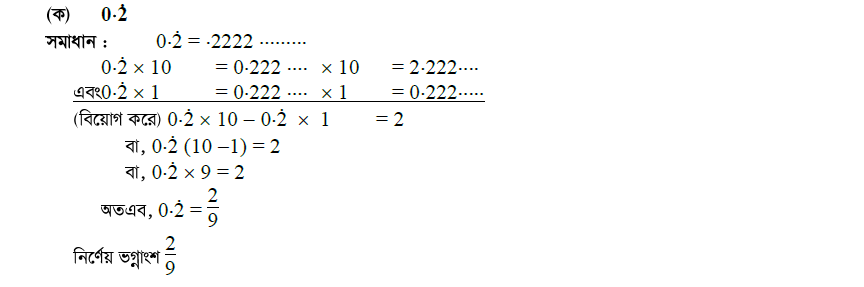
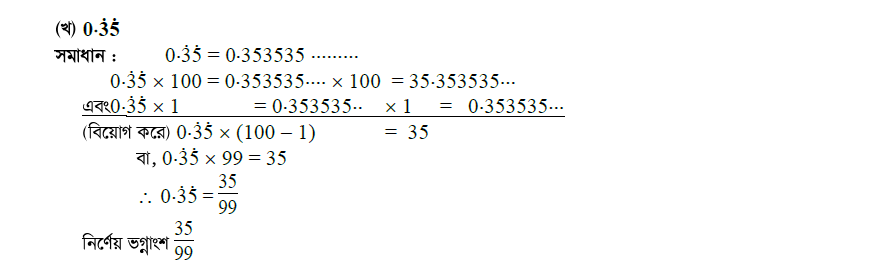
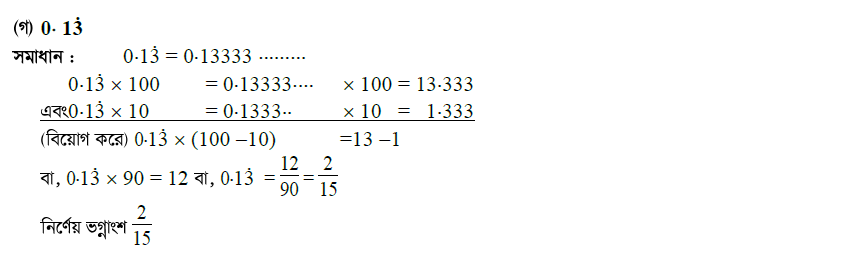
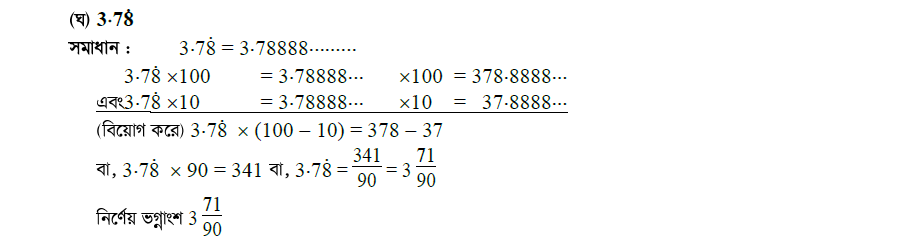
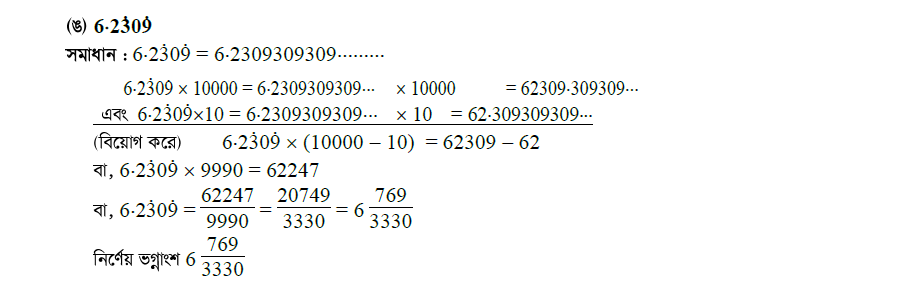
প্রশ্ন \ ৬ \ সদৃশ আবৃত্ত দশমিক ভগ্নাংশে প্রকাশ কর :
(ক) \[ 2.\overset.6, 5.2\overset.3\overset.5 \]
সমাধান : \[ 2.\overset.6, 5.2\overset.3\overset.5 \] আবৃত্ত দশমিকে অনাবৃত্ত অংশের অঙ্ক সংখ্যা যথাক্রমে 0, 1 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 1 ও 2। সদৃশ আবৃত্ত দশমিক করতে হলে প্রত্যেকটি দশমিকের অনাবৃত্ত অংশের অঙ্ক সংখ্যা 1 হবে আবৃত্ত অংশের অঙ্ক সংখ্যা হবে যথাক্রমে 1 ও 2 এর ল. সা. গু. 2। অর্থাৎ সদৃশ আবৃত্ত দশমিক সংখ্যার দশমিকের পরে মোট সংখ্যা (1 + 2) = 3 টি।
সুতরাং \[ 2.\overset.3 = 2.3\overset.3\overset.3 \]
\[ 5.2\overset.3\overset.5 = 5.2\overset.3\overset.5 \]
নির্ণেয় আবৃত্ত দশমিক ভগ্নাংশসমূহ : \[ 2.3\overset.3\overset.3, 5×2\overset.3\overset.5 \]
(খ) \[ 7.2\overset.6, 4.23\overset.7 \]
সমাধান : \[ 7.2\overset.6, 4.23\overset.7 \] আবৃত্ত দশমিকে অনাবৃত্ত অংশের অঙ্ক সংখ্যা যথাক্রমে 1 ও 2 । এখানে অনাবৃত্ত অঙ্ক সংখ্যা \[ 4.23\overset.7 \] দশমিকে বেশি এবং এ সংখ্যা হলো 2। তাই সদৃশ আবৃত্ত দশমিক করতে হলে প্রত্যেকটি দশমিকের অনাবৃত্ত অংশের অঙ্ক সংখ্যা 2 হবে। \[ 7.2\overset.6, 4.23\overset.7 \] আবৃত্ত দশমিকে আবৃত্ত অংশের সংখ্যা যথাক্রমে 1 ও 1 । 1 ও 1 এর ল.সা.গু হলো 1। তাই সদৃশ আবৃত্ত দশমিক করতে হলে প্রত্যেকটি দশমিকের আবৃত্ত অংশের অঙ্ক সংখ্যা 1 হবে।
সুতরাং \[ 7.2\overset.6 = 7.26\overset.6 \],
\[ 4.23\overset.7 = 4.23\overset.7 \]
নির্ণেয় আবৃত্ত দশমিক ভগ্নাংশসমূহ : \[ 7×26\overset.6, 4.23\overset.7 \]
(গ) \[ 5.\overset.7, 8.\overset.3\overset.4, 6. \overset.24\overset.5 \]
সমাধান : \[ 5.\overset.7, 8.\overset.3\overset.4, 6. \overset.24\overset.5 \] আবৃত্ত দশমিকে অনাবৃত্ত অংশের অঙ্ক সংখ্যা যথাক্রমে, 0, 0 ও 0। এখানে অনাবৃত্ত অঙ্ক সংখ্যা 0। তাই সদৃশ আবৃত্ত দশমিক করতে হলে প্রত্যেকটি দশমিকের অনাবৃত্ত অংশের অঙ্ক সংখ্যা 0 হবে। \[ 5.\overset.7, 8.\overset.3\overset.4, ও 6. \overset.24\overset.5 \] আবৃত্ত দশমিকে আবৃত্ত অংশের সংখ্যা যথাক্রমে 1, 2 ও 3। 1, 2 ও 3 এর ল.সা.গু হলো 6। তাই সদৃশ আবৃত্ত দশমিক করতে হলে প্রত্যেকটি দশমিকের আবৃত্ত অংশের অঙ্ক সংখ্যা 6 হবে।
সুতরাং \[ 5.\overset.7 = 5.\overset.77777\overset.7 \] ,
\[ 8.\overset.3\overset.4 = 8.\overset.3343\overset.4 \] ও
\[ 6. \overset.24\overset.5 = 6.\overset.24524\overset.5 \]
নির্ণেয় আবৃত্ত দশমিক ভগ্নাংশসমূহ : \[ 5.\overset.77777\overset.7, 8.\overset.3343\overset.4 , 6.\overset.24524\overset.5 \]
(ঘ) 12.32, \[ 2.1\overset.9, 4.32\overset.5\overset.6 \]
সমাধান : 12.32 এ অনাবৃত্ত অংশ বলতে দশমিক বিন্দুর পরে 2 টি অঙ্ক এখানে আবৃত্ত অংশ নেই। \[ 2.1\overset.9 \] এ অনাবৃত্ত অংশের অঙ্ক সংখ্যা 1, \[ 4.32\overset.5\overset.6 \] এ অনাবৃত্ত অংশের অঙ্ক সংখ্যা 2 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 2। এখানে অনাবৃত্ত অংশের অঙ্ক সংখ্যা সবচেয়ে বেশি হলো 2 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা 1 ও 2 এর ল.সা.গু 2। প্রত্যেকটি দশমিকের অনাবৃত্ত অংশের অঙ্ক সংখ্যা হবে 2 এবং আবৃত্ত অংশের অঙ্ক সংখ্যা হবে 2।
∴ 12.32 = \[12.32\overset.0\overset.0 \]
\[ 2.1\overset.9 = 2.19\overset.9\overset.9 \]
ও \[ 4.32\overset.5\overset.6 = 4.32\overset.5\overset.6 \]
নির্ণেয় আবৃত্ত দশমিক ভগ্নাংশসমূহ : \[ 12.32\overset.0\overset.0 , 2.19\overset.9\overset.9 4.32\overset.5\overset.6 \]



