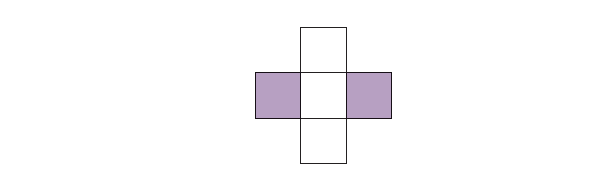Here’s what you’ll learn in the Singapore Math Level 2A & 2B – Unit 12: Fractions worksheet. We’ve provided answers to 82 questions, which include: (a) Identifying pictures split into equal parts (b) Writing numbers based on pictures (c) Coloring pictures according to numbers (d) Filling in blanks (e) Making a whole (f) Comparing smaller or larger (g) Adding and subtracting (h) Solving story problems. All of this focuses on fractions. Let’s check out the answers. Stay with us for accurate results. Thank you!
Singapore Math Level 2A & 2B – Unit 12: Fractions solution step by step
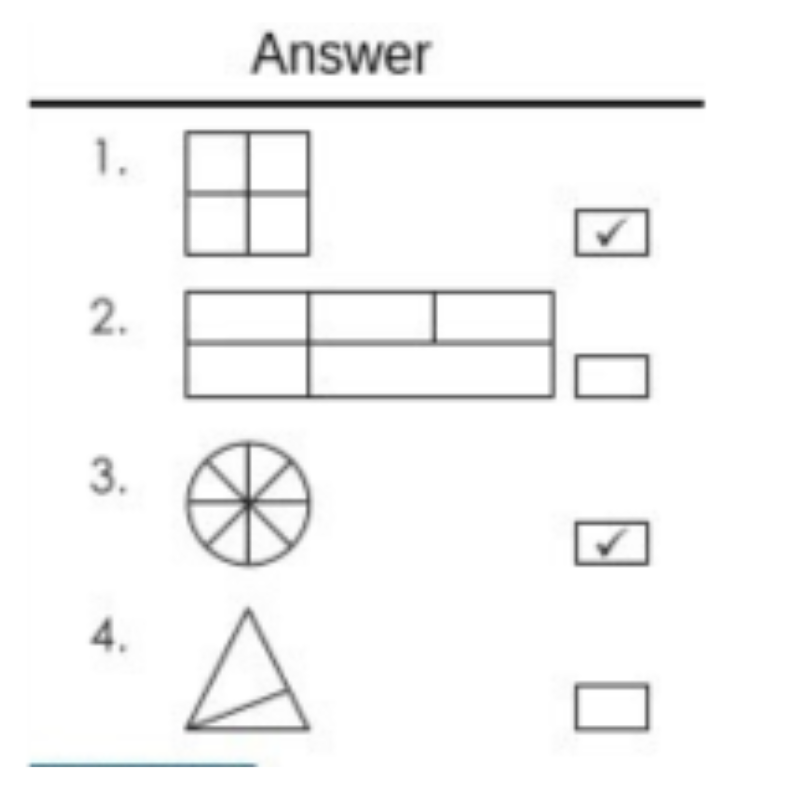
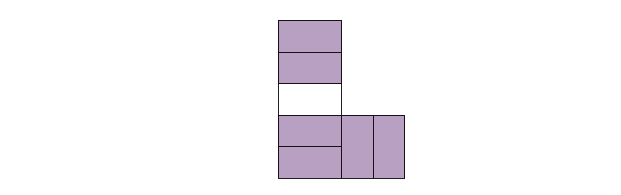
If the shape is divided into equal parts, put a check mark (✓) in the box provided next to each shape.
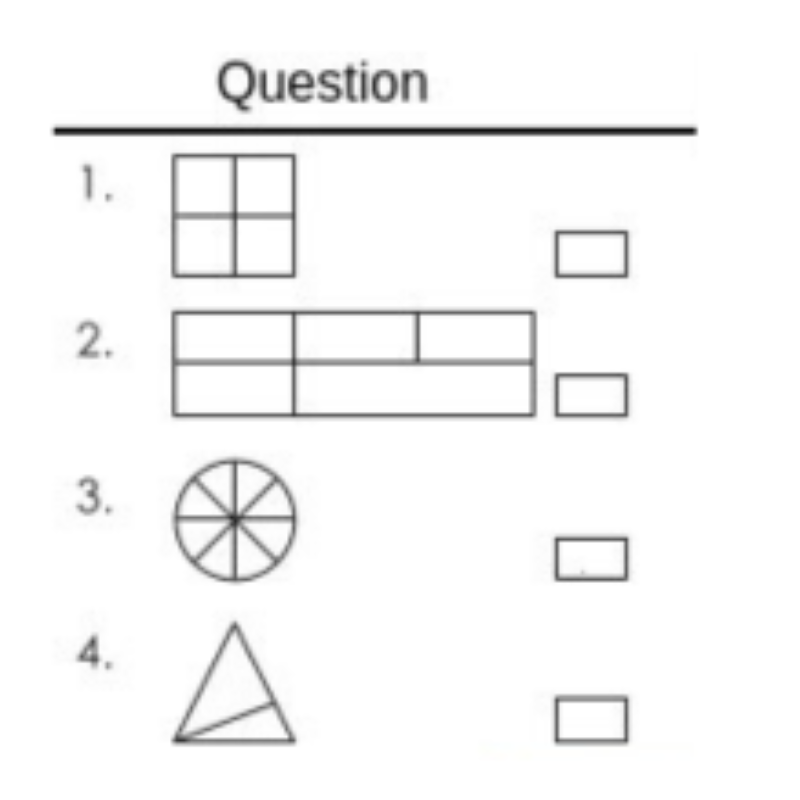
Solution(1-4):
Get the answer in the picture below:
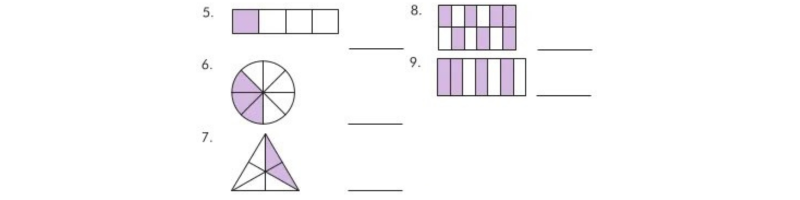
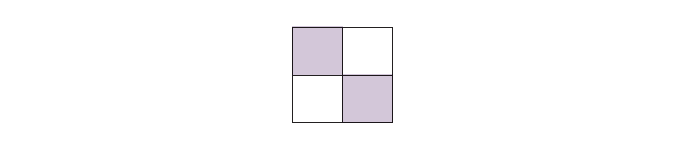
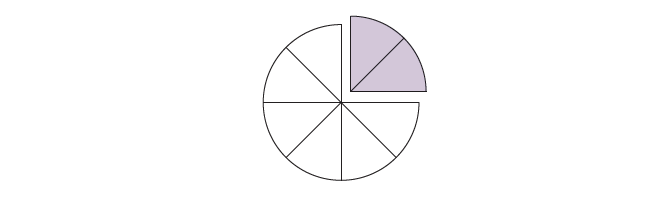
Write the fraction on the line based on the shaded parts of each figure.
Solution(5-9):
5. \[\frac14\]
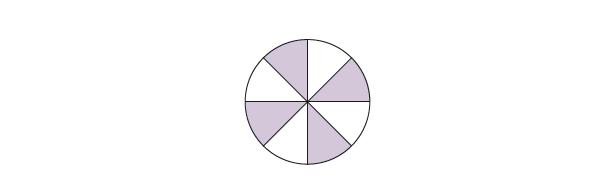
6. \[\frac38\]
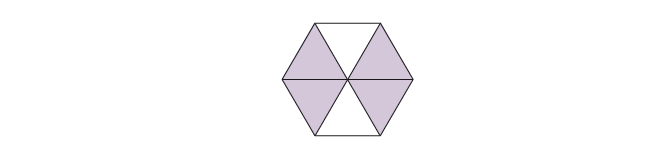
7. \[\frac26\]
8. \[\frac{7}{12}\]
9. \[\frac47\]
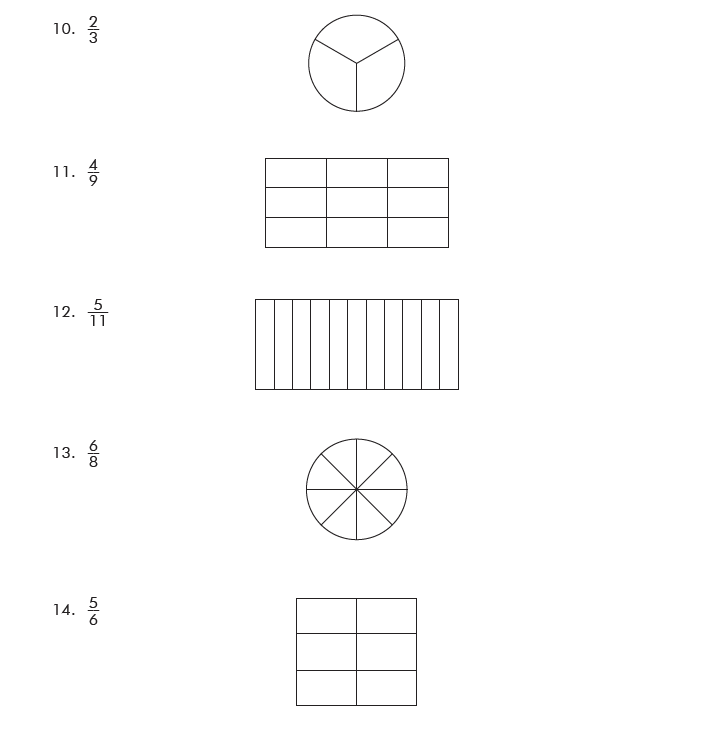
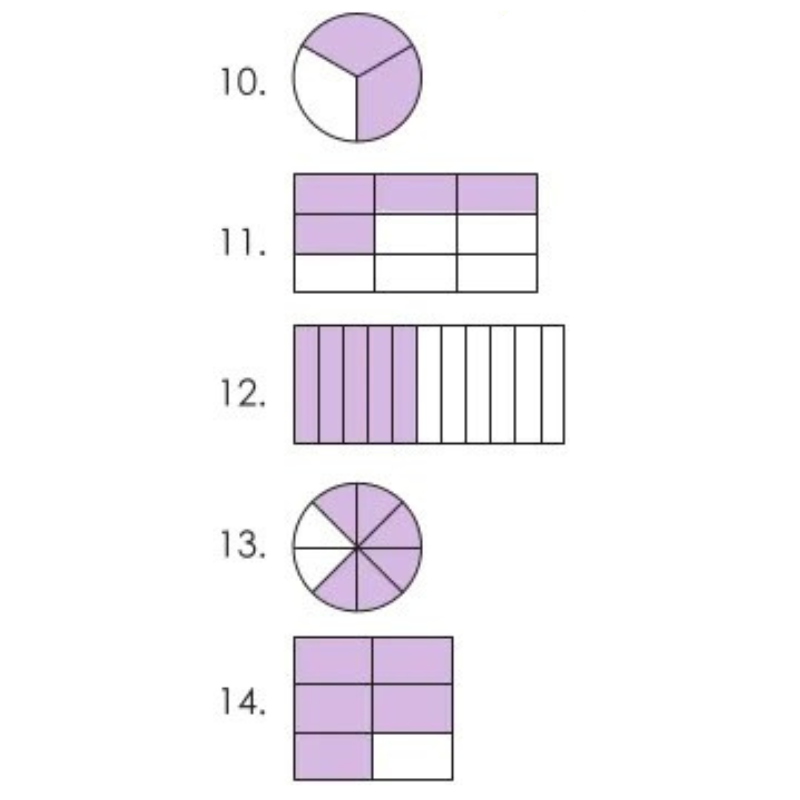
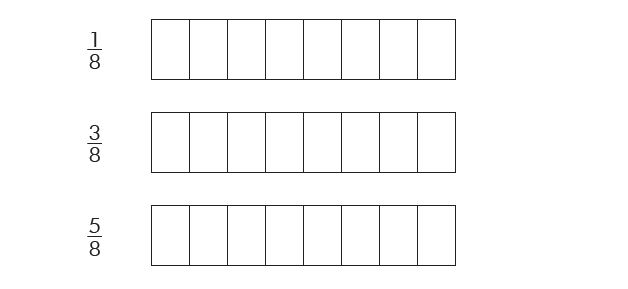
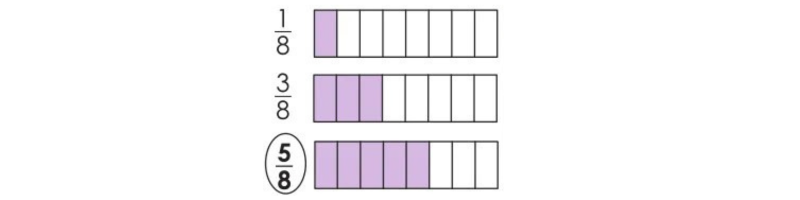
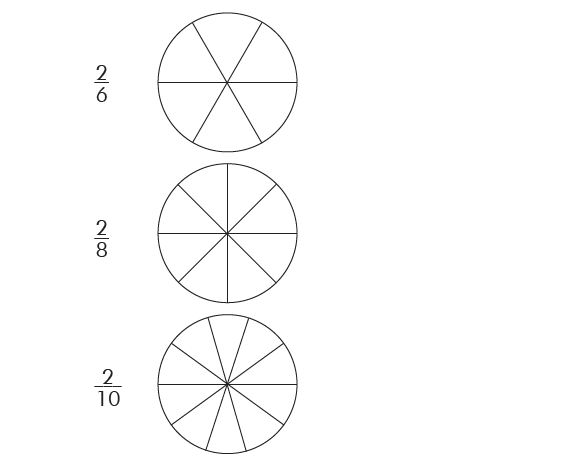
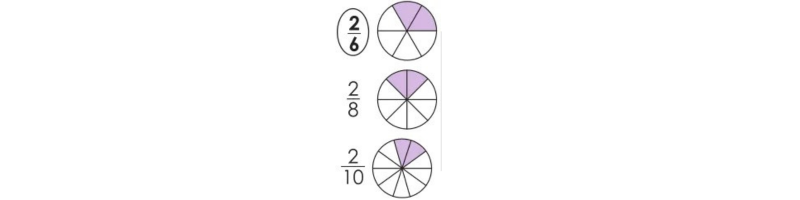
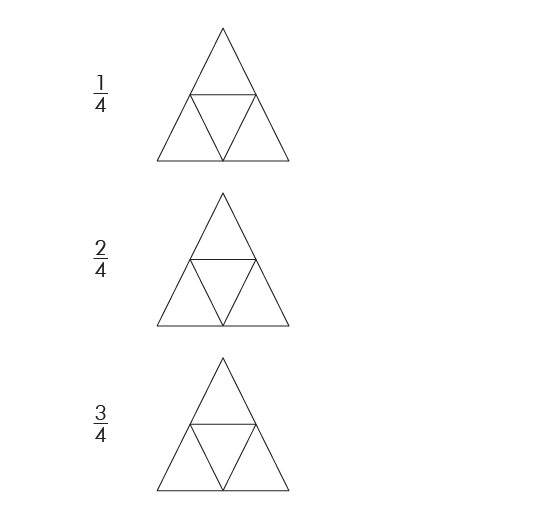
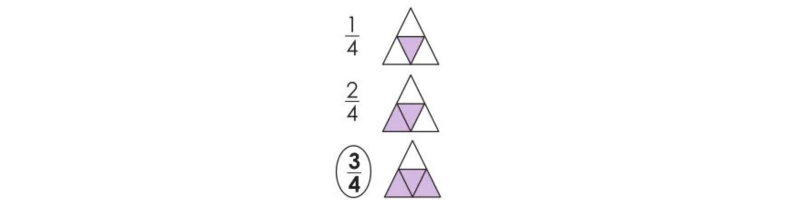
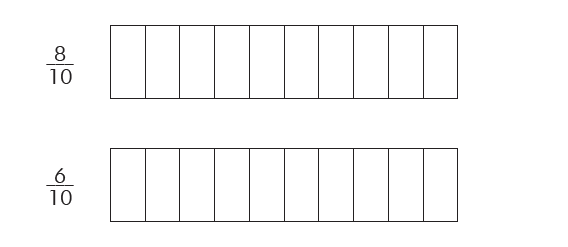
Shade the parts of each figure (10-14) as per the fractions below.
Solution(10-14):
Fill in each blank as per shade of each figure.
15.
Solution(15):
(a) 2
(b) 4
(c) \[\frac24\]
(d) \[\frac24\]
16.
Solution(16):
(a) 4
(b) 6
(c) \[\frac46\]
(d) \[\frac26\]
17.
Solution(17):
(a) 4, 8
(b) \[\frac48\]
18.
Solution(18):
(a) 2, 5
(b) \[\frac25\]
19.
Solution(19):
a) 6, 7
(b) \[\frac67\]
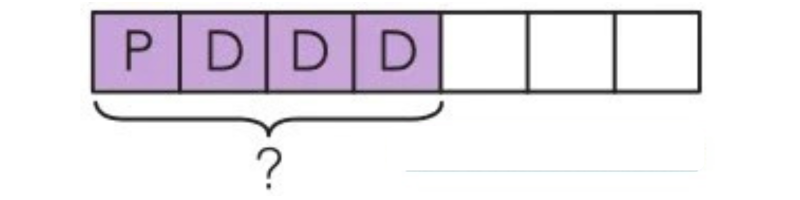
20. Hiroshi cuts a bread into 8 equal parts. His sister eats 2 parts.
Solution(20):
(a) 6 parts of the bread are left.
(b) The fraction of the bread that her brother eats is \[\frac28\] .
(c) The fraction of the bread left is \[\frac68\] .
(d) \[\frac28\] and \[\frac68\] make a whole.
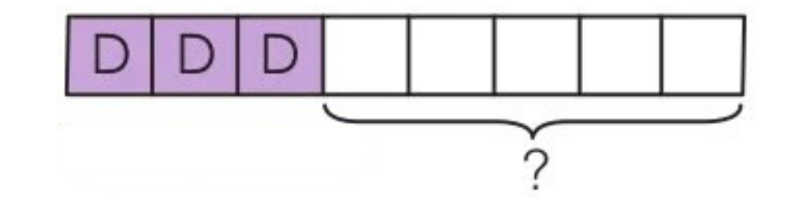
21. Lisa cuts a cake into 5 equal parts. She eats 3 parts.
Solution(21):
(a) 2 parts of the cake are left.
(b) The fraction of the cake that Lisa eats is \[\frac35\] .
(c) The fraction of the cake left is \[\frac25\] .
(d) \[\frac35\] and \[\frac25\] make a whole.
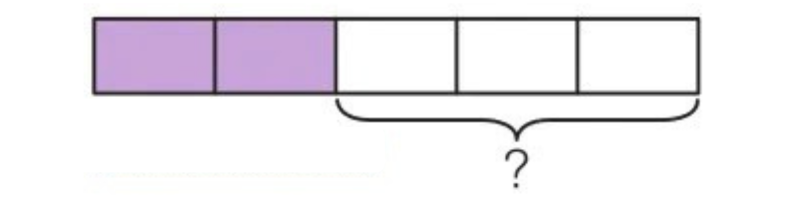
Find another fraction that make a whole with the given fraction.
22. ——— and \[\frac13\] make a whole.
23.——— and\[\frac12\] make a whole.
24.\[\frac37\]and ——- make a whole.
25.———and\[\frac4{11}\] make a whole.
26.——— and\[\frac9{12}\] make a whole.
27.\[\frac25\] and ———make a whole.
28.\[\frac68\] and ———make a whole.
29.\[\frac39\] and ———make a whole.
30. ———and\[\frac14\] make a whole.
31. ———and\[\frac16\] make a whole.
Solution(22-31):
22. \[\frac23\]
23. \[\frac12\] 1
24. \[\frac47\]
25. \[\frac7{11}\]
26. \[\frac3{12}\]
27. \[\frac35\]
28. \[\frac28\]
29. \[\frac69\]
30. \[\frac34\]
31. \[\frac56\]
Find the larger fraction in each pair.
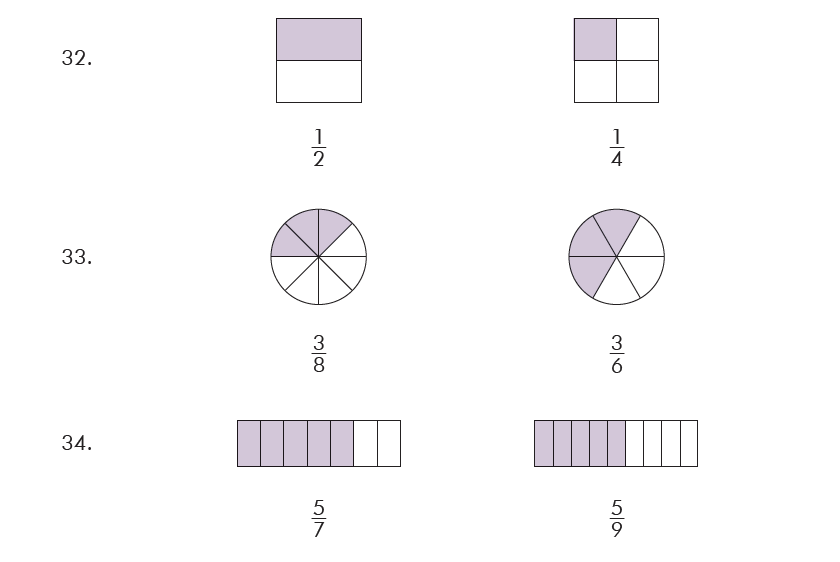
Solution(32-34):
32. Compare numerator and denominator of \[\frac12\] and \[\frac14\] .
1 = 1
2 < 4
So, \[\frac12\] > \[\frac14\]
33. Compare numerator and denominator of \[\frac38\] and \[\frac36\] .
3 = 3
8 > 6
So, \[\frac38\] <\[\frac36\]
34. Compare numerator and denominator of \[\frac57\] and \[\frac59\] .
5 = 5
7 < 9
So, \[\frac57\] >\[\frac59\]
Find the smaller fraction in each pair.
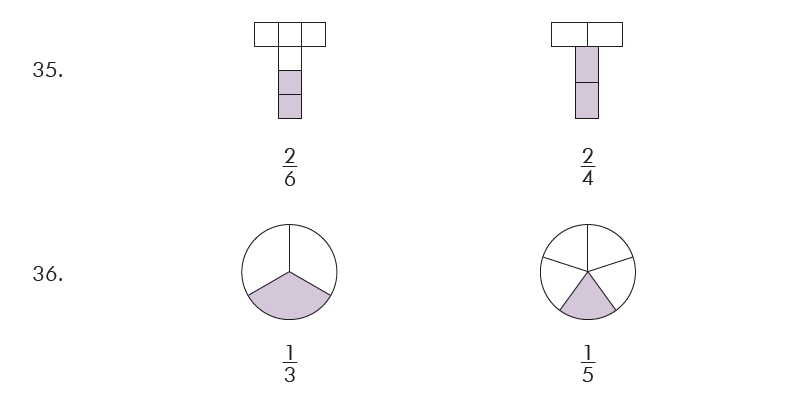
Solution(35-37):
35. Compare numerator and denominator of \[\frac57\] and \[\frac59\].
2=2
6>4
So, 2/6 \[\frac26\] < \[\frac24\]
36. Compare numerator and denominator of \[\frac57\] and \[\frac59\] .
1=1
5<3
So, \[\frac15\] < \[\frac13\]
37. Compare numerator and denominator of \[\frac57\] and \[\frac59\] .
6=6
12>10
So, \[\frac6{12}\] <\[\frac6{10}\]
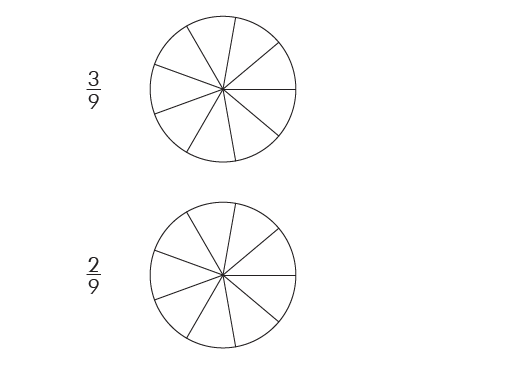
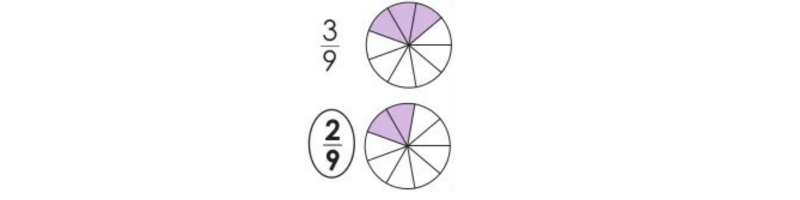
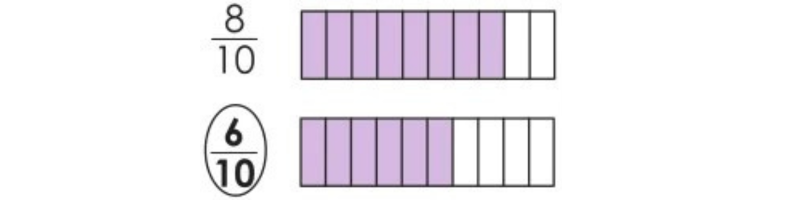
Color the correct part(s) of each figure to show the fractions. Then, circle the largest fraction in each set.
38.
40.
Solution(40):
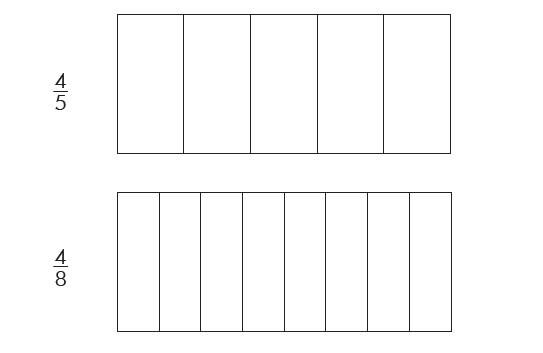
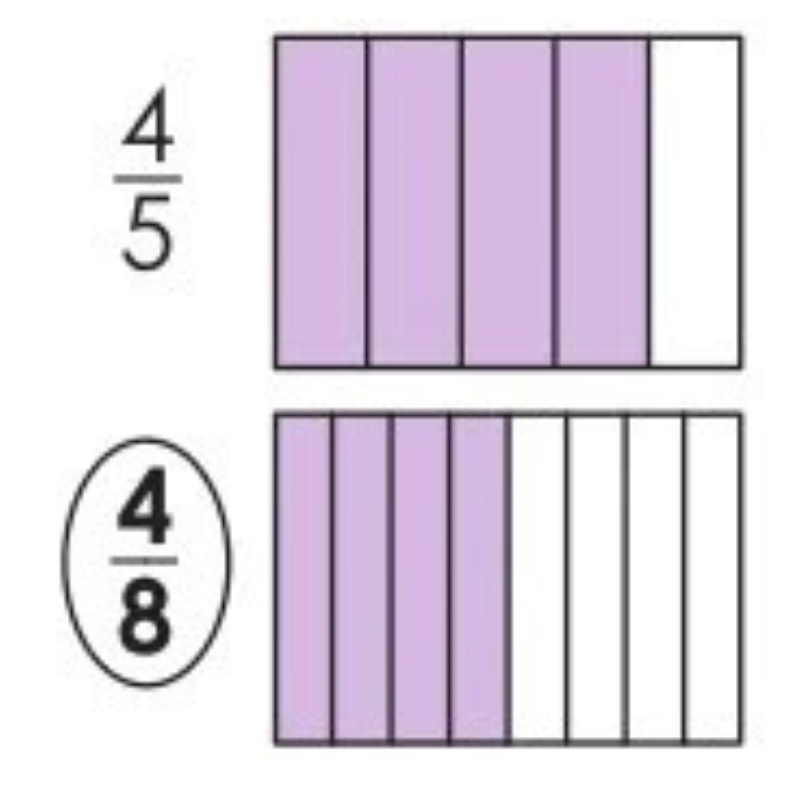
Color the part(s) of each figure to show the fractions. Then, circle the smaller fraction in each pair.
41.
Solution(41):
42.
Solution(42):
43.
Solution(43):
Find the smaller fraction in each pair.
44. \[\frac15, \frac13\]
45. \[\frac26, \frac28\]
46. \[\frac48, \frac38\]
Solution(44-46):
44. \[\frac15\]
45. \[\frac28\]
46. \[\frac38\]
Find the larger fraction in each pair.
47. \[\frac23, \frac13\]
48. \[\frac48, \frac45\]
49. \[\frac7{10}, \frac7{11}\]
Solution(47-49):
47. \[\frac23\]
48. \[\frac45\]
49. \[\frac7{10}\]
Find the largest fraction in each set.
50. \[\frac35, \frac45, \frac55 \]
51. \[\frac1{10}, \frac1{11}, \frac1{12} \]
52. \[\frac57, \frac58, \frac59 \]
Solution(50-52):
50. \[\frac55 \]
51. \[\frac1{10} \]
52. \[\frac57 \]
Find the smallest fraction in each set.
53. \[\frac13, \frac14, \frac15 \]
54. \[\frac77, \frac47, \frac57 \]
55. \[\frac59, \frac69, \frac39 \]
Solution(53-55):
53. \[\frac15 \]
54. \[\frac47 \]
55. \[\frac39 \]
Arrange the fractions from largest to smallest in each set.
56. \[\frac16, \frac56, \frac36 \]
57. \[\frac28, \frac23, \frac29 \]
58. \[\frac4{11}, \frac4{12}, \frac4{10} \]
Solution(56-58):
56. \[\frac56, \frac36, \frac16 \]
57. \[\frac22, \frac28, \frac29 \]
58. \[\frac4{10}, \frac4{11}, \frac4{12} \]
Arrange the fractions from smallest to largest in each set.
59. \[\frac{1}{10} —— \frac{1}{12} ——- \frac{1}{11} \]
60. \[\frac36——\frac35 ——– \frac39 \]
61. \[\frac5{10}, \frac59, \frac 5{12}\]
Solution(59-61):
59. \[\frac1{12} —– \frac1{11} —– \frac1{10} \]
60. \[\frac39 —– \frac36 —– \frac35 \]
61. \[\frac5{12} —– \frac5{10} —— \frac59 \]
Add these fractions.
62. \[\frac18 + \frac28 \] = ——————-
Solution(62):
\[\frac18 + \frac28 \]
= \[\frac{1+2}8 \]
= \[\frac{3}8 \]
63. \[\frac1{10} + \frac6{10} \] = ——————-
Solution(63):
\[\frac1{10} + \frac6{10} \]
= \[\frac{1 + 6}{10} \]
= \[\frac{7}{10} \]
64. \[\frac3{12} + \frac7{12} \] = ——————-
Solution(64):
\[\frac3{12} + \frac7{12} \]
= \[\frac{3 + 7}{12} \]
= \[\frac{10}{12} \]
65. \[\frac2{7} + \frac4{7} \] = ——————-
Solution(65):
\[\frac2{7} + \frac4{7} \]
= \[\frac{2 + 4}{7} \]
= \[\frac{6}{7} \]
66. \[\frac1{9} + \frac59 + \frac29\] = ——————-
Solution(66):
\[\frac1{9} + \frac59 + \frac29\]
= \[\frac{1 + 5 + 2}{9} \]
= \[\frac{8}{9} \]
67. \[\frac15+ \frac25+ \frac15\] = ——————-
Solution(67):
\[\frac15+ \frac25+ \frac15\]
= \[\frac{1 + 2 + 1}5 \]
= \[\frac{4}5 \]
68. \[\frac26+ \frac16+ \frac16\] = ——————-
Solution(68):
\[\frac26+ \frac16+ \frac16\]
= \[\frac{2 + 1 + 1}6 \]
= \[\frac{4}6 \]
69. \[\frac2{11}+ \frac1{11}+ \frac3{11}\] = ——————-
Solution(69):
\[\frac2{11}+ \frac1{11}+ \frac3{11}\]
= \[\frac{2 + 1 + 3}{11} \]
= \[\frac{6}{11} \]
Subtract these fractions.
70. \[\frac34 – \frac14 \] = ——————-
Solution(70):
\[\frac34 – \frac14 \]
= \[\frac{3 – 1}4 \]
= \[\frac{2}4 \]
71. \[\frac59 – \frac39 \] = ——————-
Solution(71):
\[\frac59 – \frac39 \]
= \[\frac{5 – 3}9 \]
= \[\frac{2}9 \]
72. \[\frac67 – \frac17 \] = ——————-
Solution(72):
\[\frac67 – \frac17 \]
= \[\frac{6 – 1}7 \]
= \[\frac{5}7 \]
73. \[1 – \frac1{10} \] = ——————-
Solution(73):
\[1 – \frac1{10} \]
= \[{10}{10} – \frac1{10} \]
= \[{10 – 1}{10} \]
= \[{9}{10} \]
74. \[\frac56 – \frac16 – \frac26 \] = ——————-
Solution(74):
\[\frac56 – \frac16 – \frac26 \]
= \[{5 – 1 – 2}6 \]
= \[{5 – 3}6 \]
= \[{2}6 \]
75. \[\frac{10}{11} – \frac{3}{11} – \frac{4}{11}\] = ————–
Solution(75):
\[\frac{10}{11} – \frac{3}{11} – \frac{4}{11}\]
= \[\frac{10 – 3 – 4}{11} \]
= \[\frac{10 – (3 + 4)}{11} \]
= \[\frac{10 – 7}{11} \]
= \[\frac{3}{11} \]
76. \[\frac{6}{8} – \frac{1}{8} – \frac{2}{8}\] = ——————-
Solution(76):
\[\frac{6}{8} – \frac{1}{8} – \frac{2}{8}\]
= \[\frac{6 – 1 – 2}{8}\]
= \[\frac{6 – (1 + 2)}{8}\]
= \[\frac{6 – 3}{8}\]
= \[\frac{3}{8}\]
77. \[\frac{10}{12} – \frac{2}{12} – \frac{5}{12}\] = ————
Solution(77):
\[\frac{10}{12} – \frac{2}{12} – \frac{5}{12}\]
= \[\frac{10 – 2 – 5}{12} \]
= \[\frac{10 – (2 + 5)}{12} \]
= \[\frac{10 – 7}{12} \]
= \[\frac{3}{12} \]
Solve the following story problems.
78. Tenny cuts an apple into 5 parts. His brother eats 2 pieces of the apple. What fraction of the apple is left?
Solution(78):
\[\frac{5}{5} – \frac{2}{5} \]
= \[\frac{5 – 2}{5} \]
= \[\frac{3}{5} \]
\[\frac{3}{5} \] of the apple is left.
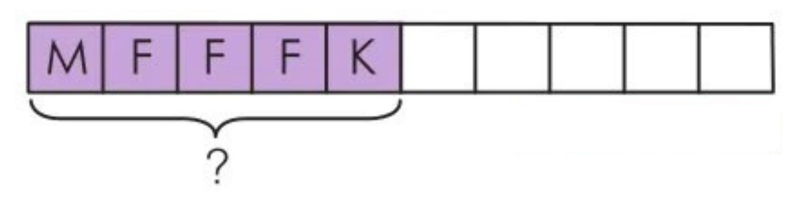
79. Penny’s Mother eats \[\frac{1}{10} \] of a Cake. Penny’s Father eats \[\frac{3}{10} \] of the Cake. Penny eats \[\frac{1}{10} \] of the cake. What fraction of the cake have they (father+mother+penny) eaten?
Solution(79):
M: Mom
F: Dad
K: Penny
\[\frac{1}{10} + \frac{3}{10} + \frac{1}{10}\]
= \[\frac{1 + 3 + 1}{10} \]
= \[\frac{5}{10} \]
They have eaten \[\frac{5}{10} \] of the pizza.
80. Kaylee used \[\frac{1}{7} \] of her weekly allowance to buy a pencil case. She used another \[\frac{3}{7} \] of it to buy some drawing materials. What fraction of her weekly allowance did Kaylee use?
Solution(80):
P: Pencil case
D: Drawing materials
\[\frac{1}{7} + \frac{3}{7} \]
= \[\frac{1 + 3}{7} \]
= \[\frac{4}{7} \]
She used \[\frac{4}{7} \] of her weekly allowance.
81. Aunt Carol made a pitcher of orange juice. Her children drank \[\frac{3}{8} \] of the orange juice. What fraction of the pitcher of orange juice was left?
Solution(81):
D: Drank
\[\frac{8}{8} – \frac{3}{8} \]
= \[\frac{8 – 3}{8} \]
= \[\frac{5}{8} \]
\[\frac{5}{8} \] of the pitcher of orange juice was left.
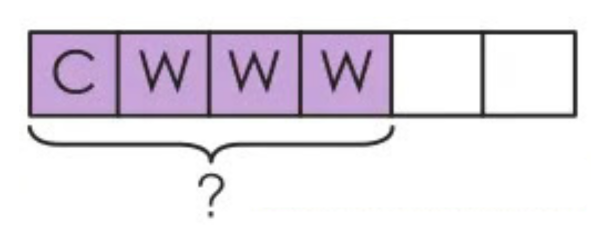
82. \[\frac{1}{6} \] of the people at a party are boys. \[\frac{3}{6} \] of the people are girls. The remaining people are adults. What fraction of the people at the party are boys and girls?
Solution(82):
C: boys
W: girls
\[\frac{1}{6} + \frac{3}{6} \]
= \[\frac{1 + 3}{6} \]
= \[\frac{4}{6} \]
\[\frac{4}{6} \] of the people at the party are children and women.