“Class eight Math- অষ্টম শ্রেণি গণিত অনুশীলনী ৮ সমাধান” শিক্ষার্থীদের জন্য একটি গুরুত্বপূর্ণ গাইড। এই সমাধানটি বিভিন্ন ধরনের সমস্যা ও ধারণা সহজভাবে বিশ্লেষণ করে, যা ছাত্রদের গণিতের মৌলিক ধারণা বুঝতে এবং পরীক্ষার প্রস্তুতি নিতে সহায়তা করে।
Class eight Math- অষ্টম শ্রেণি গণিত অনুশীলনী ৮ সমাধান
১. সামন্তরিকের জন্য নিচের কোনটি সঠিক?
ক. বিপরীত বাহুগুলো অসমান্তরাল
খ. একটি কোণ সমকোণ হলে, তা আয়ত
গ. বিপরীত বাহুদ্বয় অসমান
ঘ. কর্ণদ্বয় পরস্পর সমান
উত্তরঃ খ
২. নিচের কোনটি রম্বসের বৈশিষ্ট্য?
ক. কর্ণদ্বয় পরস্পর সমান
খ. প্রত্যেক কোণই সমকোণ
গ. বিপরীত কোণদ্বয় অসমান
ঘ. প্রত্যেকটি বাহুই সমান
উত্তরঃ ঘ
৩. i. চতুর্ভুজের চার কোণের সমষ্টি চার সমকোণ।
ii. আয়তের দুইটি সন্নিহিত বাহু সমান হলে তা একটি বর্গ।
iii. প্রত্যেকটি রম্বস একটি সামন্তরিক।
উপরের তথ্য অনুসারে নিচের কোনটি সঠিক?
ক. i ও ii খ. i ও iii গ. ii ও iii ঘ. i, ii ও iii
উত্তরঃ ঘ
৪. নিচের চিত্রটি লক্ষ্য করঃ

PAQC চতুর্ভুজের PPA=CQ এবং PA।।CQ.
∠A ও ∠C এর সমদ্বিখন্ডক যথাক্রমে AB ও CD হলে ABCD ক্ষেত্রটির নাম কী?
ক. সামন্তরিক খ. রম্বস গ. আয়ত ঘ. বর্গ
উত্তরঃ ক
৫. দেওয়া আছে, △ABC এর মধ্যমা BO কে D পর্যন্ত এমনভাবে বর্ধিত করি যেন BO=OD হয়।

প্রমাণ করতে হবে যে, ABCD একটি সামন্তরিক।
সমাধানঃ
বিশেষ নির্বচনঃ
দেওয়া আছে, △ABC এর মধ্যমা BO কে D পর্যন্ত এমনভাবে বর্ধিত করি যেন BO=OD হয়। প্রমাণ করতে হবে যে, ABCD একটি সামন্তরিক।
প্রমাণঃ
△ABC এ
CO=AO [BO মধ্যমা বলে]
এখন, △COB ও △DOA এ
CO=AO [BO মধ্যমা বলে]
BO=DO [শর্তানুসারে]
∠COB=∠DOA [বিপ্রতীপ কোণ]
∴△COB ≅ △DOA
তাহলে, AD=CB
অনুরুপভাবে পাই, CD=AB
∴ ABCD একটি সামন্তরিক (প্রমাণিত)
৬. প্রমাণ কর যে, সামন্তরিকের একটি কর্ণ একে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক যার একটি কর্ণ AC. প্রমাণ করতে হবে যে, AC কর্ণ ABCD সামন্তরিককে সমান দুই ভাগে ভাগ করে অর্থাৎ △ABC ≅ △ADC.
প্রমাণঃ
যেহেতু ABCD সামন্তরিক সেহেতু AB।।DC ও AD।।BC
এখন, AB।।DC ও AC তাদের ছেদক
∴∠BAC=∠DCA [একান্তর কোণ]
আবার, AD।।BC ও AC তাদের ছেদক
∴∠DAC=∠BCA [একান্তর কোণ]
এখন, △ADC ও △ABC এ
∠BAC=∠DCA
∠DAC=∠BCA
AC সাধারণ বাহু
∴△ADC ≅ △ABC (প্রমাণিত)
৭. প্রমাণ কর যে, চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল হলে, তা একটি সামন্তরিক।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি চতুর্ভুজ। এর AD=BC, AB=CD এবং AD।।BC, AB।।CD. প্রমাণ করতে হবে যে, ABCD একটি সামন্তরিক।
অঙ্কনঃ
A, C যোগ করি।
প্রমাণঃ
AB।।DC ও AC তাদের ছেদক
∴∠BAC=∠DCA [একান্তর কোণ]
আবার, AD।।BC ও AC তাদের ছেদক
∴∠DAC=∠BCA [একান্তর কোণ]
এখন, △ADC ও △ABC এ
∠BAC=∠DCA
∠DAC=∠BCA
AC সাধারণ বাহু
∴△ADC ≅ △ABC
তাহলে, ∠ABC=∠ADC
অনুরুপভাবে, ∠BAD=∠BCD
∴ABCD একটি সামন্তরিক।
৮. প্রমাণ কর যে, সামন্তরিকের কর্ণদ্বয় পরস্পর সমান হলে, তা একটি আয়ত।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD সামন্তরিকের কর্ণ AC=কর্ণ BD
প্রমাণ করতে হবে যে, ABCD একটি আয়ত।
প্রমাণঃ
△ABC ও △ADB এর মধ্যে
BC=AD
AC=BD
AB সাধারন বাহু।
∴△ABC≅△ADB
তাহলে, ∠ABC=∠BAD
এখন, যেহেতু AD।।BC এবং AB তাদের ছেদক।
∴∠ABC+∠BAD=2 সমকোণ।
∴ABCD একটি আয়ত (প্রমাণিত)
৯. প্রমাণ কর যে, চতুরভুজের কর্ণদ্বয় পরস্পর সমান হলে এবং পরস্পরকে সমকোণে সমদ্বিখন্ডিত করলে, তা একটি বর্গ।
সমাধানঃ
বিশেষ নির্বচনঃ
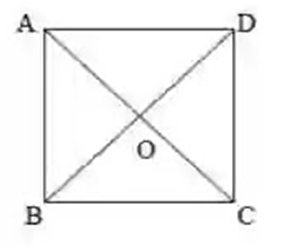
মনে করি, ABCD চতুর্ভুজের AC ও BD কর্ণ পরস্পপর সমান এবং পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করেছে। অর্থাৎ AC=BD, OA=OC, OB=OD এবং ∠AOB=∠BOC=∠COD=∠AOD=900
প্রমাণ করতে হবে যে, ABCD একটি বর্গ।
প্রমাণঃ
△AOB ও △AOD এ
OB=OD [শর্তানুসারে]
∠AOB=∠AOD [শর্তানুসারে সমকোণ]
AO সাধারণ বাহু
∴△AOB ≅ △AOD
তাহলে, AB=AD
অনুরুপভাবে পাই, AD=DC; DC=BC
অর্থাৎ, AB=AD=DC=BC
এখন, △AOB এ
∠AOB=90°
এবং OA=OB
∴∠OAB=∠OBA=45°
অনুরুপভাবে, △AOD এ ∠OAD=∠ODA=45°
∴∠BAD=∠OAB+∠OAD=45°+45°=90°
∴ABCD একটি বর্গ।
১০. প্রমাণ কর যে, আয়তের সন্নিহিত বাহুর মধ্যবিন্দুসমূহের যোগে যে চতুর্ভুজ হয়, তা একটি রম্বস।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD আয়ত। P, Q, R ও S যথাক্রমে AB, BC, CD ও AD এর মধ্যবিন্দু। P,Q; Q,R; R,S ও S, P যোগ করি। প্রমাণ করতে হবে যে, PQRS একটি রম্বস।
অঙ্কনঃ
A,C; B,D এবং S,Q; P,R যোগ করি।
প্রমাণঃ
△ABD এ AB ও AD এর মধ্যবিন্দু D ও S
∴DS।।BD এবং DS=\[\frac 12\] BD
একইভাবে পাই, QR=PS; QR= \[\frac 12\] BD
∴ PS=QR এবং PS।।QR
তাহলে আমরা একইভাবে পাই, PQ=SR; PQ।।SR
∴ PQRS একটি রম্বস (প্রমাণিত)
১১. প্রমাণ কর যে, সামন্তরিকের যেকোনো দুইটি বিপরীত কোণের সমদ্বিখন্ডক পরস্পর সমান্তরাল।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক। এর ∠A ও ∠C এর সমদ্বিখন্ডক AE ও CF যথাক্রমে DC ও AB কে E ও F বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, AE।।CF.
প্রমাণঃ
যেহেতু, AE, ∠BAD এর সমদ্বিখন্ডক
∴∠EAF=\[\frac 12\]∠BAD
অনুরুপভাবে, ∠ECF=\[\frac 12\]∠BCD
এখন, ∠BAD=∠BCD [সামন্তরিকের বিপরীত কোণ পরস্পর সমান]
∴∠EAF=∠ECF
এখন, AECF চতুর্ভুজ এ
∠EAF=∠ECF যারা পরস্পপর বিপরীত কোণ।
তাহলে, AECF চতুর্ভুজ এ ∠AEC=∠AFC
∴ AECF একটি সামন্তরিক।
∴ AE।।FC (প্রমাণিত))
১২. প্রমাণ কর যে, সামন্তরিকের যেকোনো দুইটি সন্নিহিত কোণের সমদ্বিখন্ডক পরস্পর লম্ব।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক। এর ∠BAD ও ∠ABC এর সমদ্বিখন্ডকদ্বয় পরস্পর O বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, AO ও BO পরস্পরের উপর লম্ব।
প্রমাণঃ
ABCD সামন্তরিকে,
∠BAD+∠BCD+∠ABC+ADC=360°
বা, ∠BAD+∠BAD+∠ABC+∠ABC=360° [সামন্তরিকের বিপরীত কোণগুলো পরস্পর সমান হয়]
বা, 2∠BAD+2∠ABC=360°
বা, ∠BAD+∠ABC=180°
বা, 2∠OAB+2∠OBA=180°[∠BAD ও ∠ABC এর সমদ্বিখন্ডক শর্তানুসারে]
বা, ∠OAB+∠OBA=90°……….(i)
এখন,
△ABO এ
∠OAB+∠OBA+∠AOB=180°
বা, 900+∠AOB=180° [(i) নং হতে]
বা, ∠AOB=180°-90°
বা, ∠AOB=90°
অর্থাৎ, AO ও BO পরস্পরের উপর লম্ব (প্রমাণিত)
১৩. চিত্রে, ABC একটি সমবাহু ত্রিভুজ। D, E ও F যথাক্রমে AB, BC ও AC এর মধ্যবিন্দু।

ক. প্রমাণ কর যে, ∠BDF+∠DFE+∠FEB+∠EBD=চার সমকোণ।
সমাধানঃ
মনে করি, চিত্রে, ABC একটি সমবাহু ত্রিভুজ। D, E ও F যথাক্রমে AB, BC ও AC এর মধ্যবিন্দু। প্রমাণ করতে হবে যে, ∠BDF+∠DFE+∠FEB+∠EBD=চার সমকোণ।
প্রমাণঃ
△BDE এ
∠DBE+∠BED+∠BDE=দুই সমকোণ………..(i)
আবার, △DEF এ
∠DEF+∠EFD+∠FDE=দুই সমকোণ………..(ii)
(i)+(ii) করে,
∠DBE+∠BED+∠BDE+∠DEF+∠EFD+∠FDE=চার সমকোণ
বা, ∠DBE+(∠BED+∠DEF )+(∠BDE+∠FDE)+ ∠EFD= চার সমকোণ
বা, ∠DBE+∠BEF+∠BDF+ ∠EFD= চার সমকোণ (প্রমাণিত)
খ. প্রমাণ কর যে, DF।।BC এবং DF= ½BC
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, △ABC এর D ও F যথাক্রমে AB ও AC এর মধ্যবিন্দু। D ও F যোগ করে G পর্যন্ত এমনভাবে বর্ধিত করি যেন DF=FG হয়। G, C যোগ করি। প্রমাণ করতে হবে যে, DF।।BC এবং DF= \[\frac 12\] BC
প্রমাণঃ
△ADF ও △CGF এ
DF=FG [অঙ্কনানুসারে]
AF=FC [শর্তানুসারে]
∠DFA=∠CFG [বিপ্রতীপ কোণ]
∴△ADF ≅△CGF
তাহলে, AD=CG
বা, BD=CG [AD=BD: শর্তানুসারে]
এবং, ∠DAF=∠FCG যার ছেদক AC
∴ AD।।CG
বা, BD।।CG
এখন, যেহেতু BD=CG ও BD।।CG
সেহেতু, BDGC একটি সামন্তরিক।
তাহলে, DG।।BC
বা, DF।।BC
এবং, DG=BC
বা, 2DF=BC [DF=FG বলে ]
বা, DF= \[\frac 12\] BC
∴ DF।।BC এবং DF= \[\frac 12\] BC (প্রমাণিত)
১৪. দেওয়া আছে, ABCD সামন্তরিকের AM ও CN, DB এর উপর লম্ব। প্রমাণ কর যে, ANCM একটি সামন্তরিক।

সমাধানঃ
বিশেষ নির্বচনঃ
দেওয়া আছে, ABCD সামন্তরিকের AM ও CN, DB এর উপর লম্ব। প্রমাণ করতে হবে যে, ANCM একটি সামন্তরিক।
প্রমাণঃ
△ADB এর ক্ষেত্রফল= ½.BD.AM [AM=উচ্চতা; BD=ভূমি]
△BDC এর ক্ষেত্রফল= ½.BD.CN [CN=উচ্চতা; BD=ভূমি]
এখন, △ADB এর ক্ষেত্রফল=△BDC এর ক্ষেত্রফল [ সামন্তরিকের কর্ণ সামন্তরিককে সমান ক্ষেত্রফল বিশিষ্ট দুইটি ত্রিভুজে বিভক্ত করে]
∴ \[\frac 12 \].BD.AM=\[\frac 12 \].BD.CN
বা, AM=CN
এখন, AM ও CN একই রেখা BD এর উপর লম্ব।
∴ AM।।CN
অর্থাৎ, AMCN এর বিপরীত দুইটি বাহু সমান ও সমান্তরাল।
∴ AMCN একটি সামন্তরিক (প্রমাণিত)
১৫. চিত্রে, AB=CD এবং AB।।CD

ক. AB ভুমিবিশিষ্ট দুইটি ত্রিভুজের নাম লেখ।
সমাধানঃ
AB ভুমিবিশিষ্ট দুইটি ত্রিভুজের নামঃ
△ABD ও△ ABC
খ. প্রমাণ কর যে, AD ও BC পরস্পর সমান ও সমান্তরাল।
সমাধানঃ
বিশেষ নির্বচনঃ
দেওয়া আছে, চিত্রে, AB=CD এবং AB।।CD। প্রমাণ করতে হবে যে, AD ও BC পরস্পর সমান ও সমান্তরাল।
প্রমাণঃ
△ABD ও △BDC এর মধ্যে
AB=DC [শর্তানুসারে]
BD সাধারণ বাহু
∠CDB=∠ABD [AB।।DC ও BD ছেদক বলে]
∴ △ABD≅△BDC
তাহলে, AD=BC এবং ∠ADB=∠DBC
এখন, ∠ADB=∠DBC ও BD তাদের ছেদক
∴ AD।।BC
সুতরাং, AD ও BC পরস্পর সমান ও সমান্তরাল (প্রমাণিত)
গ. দেখাও যে, OA=OC এবং OB=OD.
সমাধানঃ
বিশেষ নির্বচনঃ
দেওয়া আছে, চিত্রে, AB=CD এবং AB।।CD। দেখাতে হবে যে, OA=OC এবং OB=OD
প্রমাণঃ
△AOB ও △DOC এ
AB=DC [শর্তানুসারে]
∠AOB=∠DOC [বিপ্রতীপ কোণ]
∠DCO=∠OAB [AB।।DC ও AC ছেদক বলে]
∴ △AOB ≅ △DOC
তাহলে, OA=OC এবং OB=OD (প্রমাণিত)।
১৬. ABCD একটি সামন্তরিক। AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে।

ক) ∠BAD=70° হলে ∠ABC এর মান নির্ণয় কর।
সমাধানঃ
বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক। AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে। ∠BAD=70° । ∠ABC এর মান নির্ণয় করতে হবে।
অঙ্কনঃ
AB কে M পর্যন্ত বর্ধিত করি।
প্রমাণঃ
ABCD সামন্তরিক এর AD।।BC [সামন্তরিক বলে]
∴ ∠BAD=∠MBC=70°
কিন্তু,
∠ABC+∠MBC=180°
বা, ∠ABC+700=180°
বা, ∠ABC=180°-70°
বা, ∠ABC=110°
খ) AC=BD হলে, প্রমাণ কর যে, ABCD একটি আয়ত।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক। AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে। AC=BD হলে, প্রমাণ করতে হবে যে, ABCD একটি আয়ত।
প্রমাণঃ
△ABD ও △ABC এর মধ্যে
AC=BD [শর্তানুসারে]
AB সাধারণ বাহু
AD=BC [সামন্তরিকের বিপরীত বাহু সামন]
∴ △ABD ≅ △ABC
তাহলে, ∠DAB=∠ABC
অনুরুপভাবে আমরা পাই, ∠DAB=∠ABC=∠BCD=∠CDA
এখন চতুর্ভুজের চারটি কোন সমান হবে যদি প্রত্যেক কোনের মান 900 হয়।
∴ ∠DAB=∠ABC=∠BCD=∠CDA=90°
∴ ABCD একটি আয়ত (প্রমাণিত)
গ) AB=AD হলে, প্রমাণ কর যে, AC ও BD পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে।
সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABCD একটি সামন্তরিক। AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে। AB=AD হলে, প্রমাণ করতে হবে যে, AC ও BD পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে।
প্রমাণঃ
△ABD এ
AD=AB
∴ ∠ADB=∠ABD …..(i)
△AOD ও △AOB এ
AD=AB [শর্তানুসারে]
AO সাধারণ বাহু
∠ADO=∠ABO [(i) নং হতে]
∴ △AOD ≅ △AOB
তাহলে, OB=OD এবং ∠AOB=∠AOD
এখন, ∠AOB ও ∠AOD পরস্পর সম্পূরক কোণ
∴ ∠AOB=∠AOD=90°
একইভাবে তুলনা করে পাই, AO=OC এবং O বিন্দুতে উৎপন্ন প্রত্যেকটি কোণ সমকোণ।
∴ AC ও BD পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে (প্রমাণিত)
১৭. ABCD চতুর্ভুজে AC ও BD কর্ণদ্বয় অসমান এবং যেকোনো দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ।
ক) চিত্রসহ ঘুড়ির সংজ্ঞা দাও।

সমাধানঃ
ঘুড়ি হচ্ছে এমন একটি চতুর্ভুজ যার দুই জোড়া সন্নিহিত বাহু পরস্পর সমান।
চিত্রে ABCD একটি ঘুড়ি। যেখানে সন্নিহিত বাহু AB=AD ও BC=DC.
খ) প্রমাণ কর যে, AB=CD এবং AD=BC
সমাধানঃ

বিশেষ নির্বচনঃ
ABCD চতুর্ভুজে AC ও BD কর্ণদ্বয় অসমান এবং যেকোনো দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ। প্রমাণ করতে হবে যে, AB=CD এবং AD=BC.
প্রমাণঃ
ABCD চতুর্ভুজে যেকোনো দুটি সন্নিহিত কোণের সমষ্টি দুই সমকোণ ।
তাহলে, ∠DAB+∠ABC=180°
∴ AD।।BC
একইভাবে, AB।।DC
এখন,
△ABD ও △BDC এ
∠ADB=∠DBC [AD।।BC; BD তাদের ছেদক]
∠BDC=∠ABD [AB।।DC; BD তাদের ছেদক]
BD সাধারণ বাহু।
∴ △ABD ≅ △BDC
তাহলে, AD=BC ও AB=CD (প্রমাণিত)
গ) B ও D বিন্দু হতে AC এর উপর BP এবং DQ লম্ব আঁকা হলে, প্রমাণ কর যে, BPDQ একটি সামন্তরিক।
সমাধানঃ

বিশেষ নির্বচনঃ
ABCD চতুর্ভুজে B ও D বিন্দু হতে AC এর উপর BP এবং DQ লম্ব আঁকি। প্রমাণ করতে হবে যে, BPDQ একটি সামন্তরিক।
প্রমাণঃ
△ADQ ও △BPC এ
AD=BC [খ হতে]
∠DAQ=∠BCP [AD।।BC; AC তাদের ছেদক]
∠AQD=∠BPC=90° [অঙ্কনানুসারে]
∴ △ADQ ≅ △BPC
তাহলে, DQ=BP
এখন, DQ ও BP একই রেখা AC এর উপর লম্ব।
∴ DQ।।BP
এখন DQ=BP, DQ।।BP
∴ BPDQ একটি সামন্তরিক (প্রমাণিত)
১৮. একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 10 সেমি, 8 সেমি, এবং 5 সেমি। ঘনবস্তুর সমগ্র পৃষ্ঠের ক্ষেত্রফল নির্ণয় কর।
সমাধানঃ
দেওয়া আছে,
আয়তাকার ঘনবস্তুর দৈর্ঘ্য a=10 সেমি
প্রস্থ b=8 সেমি
উচ্চতা c=5 সেমি
আমরা জানি,
আয়তাকার সমগ্র পৃষ্টের ক্ষেত্রফল
= 2(ab+bc+ca) বর্গ একক
=2(10✕8+8✕5+5✕10) বর্গ সেমি
=2(80+40+50) বর্গ সেমি
=2✕170 বর্গ সেমি
=340 বর্গ সেমি
১৯. একটি ঘনকাকৃতি বাক্সের ধার 6.5 সেমি হলে, বাক্সটির সমগ্র পৃষ্ঠের ক্ষেত্রফল নির্ণয় কর।
সমাধানঃ
দেওয়া আছে,
ঘনকাকৃতি বাক্সের ধার a = 6.5 সেমি
∴ বাক্সটির সমগ্র পৃষ্ঠের ক্ষেত্রফল
= 6 \[a^2\]
=6✕ \[(6.5)^2\]
=253.5 বর্গ সেমি।
