Preliminary selection question for bdmo 2020
Secondary preliminary selection question
1. চিত্রে ১ থেকে শুরু করে ক্রমিক সংখ্যা গুলো একটি ত্রিভুজাকার টেবিলে লেখা হয়েছে। প্রতিটি সারিতে আগের সারির চেয়ে একটি সংখ্যা বেশি রয়েছে। যে সারিতে 25 সংখ্যাটি রয়েছে, সেই সারির সংখ্যাগুলোর যোগফল কত?
The consecutive counting numbers are written in a triangular table, as shown, with one more number in each successive row.What is the sum of the numbers in the row that contains 25?
2. একটি সমতলে 6 টি ভিন্ন ভিন্ন সরলরেখা একটি বর্গকে বিভিন্ন ভাগে ভাগ করে। বর্গটিকে ৬টি সরলরেখা সর্বনিম্ন কতটি ভাগে ভাগ করতে পারবে?
In a plane, 6 distinct lines intersect the interior of a square forming regions within the square. What is the minimum number of regions that can be formed?
3. নওশাদের থেকে জয়দীপের 21 টাকা বেশি আছে এবং নওশাদের থেকে রুবারের 15 টাকা কম আছে। তিনজন সিদ্ধান্ত নিল যে টাকা গুলো নিজেদের মধ্যে সমান ভাগে ভাগ করে নিবে। সমবন্টনের ফলে জয়দীপের কত টাকা কমে গেল?
Joydip has 21 more taka than Nowshad.Nowshad has 15 more taka than Rubab.All of them decide to split their money so each of three will have the same amount of money.How many taka Joydip lose?
4. এমন সকল মৌলিক সংখ্যা p এর কর যেন 17p + 7 একটি মৌলিক সংখ্যা হয়।
Find the prime number p such that 17p+7 is also a prime number
5. 2020 এর কতগুলো যৌগ উৎপাদক আছে?
How many even divisors 2020 have?
6. N একটি পূর্ণসংখ্যা যার 7 টি উৎপাদক আছে। এই উৎপাদকগুলোর মধ্যে 4 টি আবার নিজেরই পূর্ণসংখ্যা। N-এর সর্বনিম্ন মান কত?
N is a perfect square that has 7 factors. 4 of these factors are themselves perfect squares. What is the smallest possible value of N?
7. x এবং y ধনাত্মক পূর্ণসংখ্যা এবং xxx – 8y = 4x । x যদি 4 এর গুণিতক হয়, তবে y-এর সর্বনিম্ন মান কত?
x and y are positive integers and x×x-8y=4x. If x is not a multiple of 8, then what is the minimum possible value for y?
8. ট্রাপিজিয়াম ABCD এর AB এবং CD পরস্পর সমান্তরাল বাহু। P এবং Q, যথাক্রমে AC এবং BD কর্ণের মধ্যবিন্দু এবং CD = 2020 এবং AB = 1010 তবে PQ-এর দৈর্ঘ্য কত?
Let AB and CD be the parallel sides of trapezium ABCD.Let P and Q be the midpoint of the diagonals AC and BD.If CD=2020 and AB=1010 then what is the length of PQ?
9. T(1) = 3,T(2) = 6 এবং যখন n -এর মান 2-এর চেয়ে বড়, তখন T(n) = T(n-1) – T(n-2) + 5। তাহলে T(2020)-এর মান কত?
T(1)=3; T(2)=6 and T(n)=T(n-1)-T(n-2)+5 when n>2.Find T(2020)
10. একটি বৃত্তের জ্যা AB-এর মধ্যবিন্দু C এবং বৃত্তচাপ AB-এর মধ্যবিন্দু D। যদি AB = 36 এবং CD = 6 হয়, তাহলে বৃত্তের ব্যাসার্ধ কত?
C is the midpoint of chord AB and D is the midpoint of arc AB.Given that AB=36 unit and CD=6 unit then What is the radius of circle?
Higher Secondary preliminary selection question
1. প্রথম 2020 টি ক্রমিক ধনাত্মক পূর্ণসংখ্যার যোগফলকে 4 দিয়ে ভাগ করলে ভাগশেষ কত হবে?
What is the remainder if the summation of first 2020 consecutive positve numbers is divided by 4?
2. একটি সমতলে 6টি ভিন্ন বিন্দু সরলরেখা একটি বৃত্তকে বিভিন্ন ভাগে ভাগ করে। বৃত্তটিকে 6টি সরলরেখা সর্বনিম্ন কতটি ভাগে ভাগ করতে পারে?
In a plane, 6 distinct lines intersect the interior of a circle forming regions within the circle. What is the minimum number of regions that can be formed?
3. সকাল দা ফিফা’19 খেলার সময় গোল দেওয়ার চেষ্টা করছে। প্রথমে তার গোল দেওয়ার সম্ভাবনা 20%। আর প্রতিবার গোল মিস করলে সকাল দার সম্ভাবনা 5% বেড়ে যায়। অর্থাৎ, প্রথম বারে যদি সকাল দা গোল মিস করে তাহলে দ্বিতীয় বারে গোল দেবার সম্ভাবনা 25% হয়ে যায়। ন্যূনতম কতবার চেষ্টা করলে সকাল দা নিশ্চিতভাবে ফিফা’19 এ গোল দিতে পারবে?
Sakal is attempting to score a goal in FIFA’19. On his first attempt, he has a 20% chance of success. Sakal’s likelihood of success improves by 5% after each failed attempt. For example, his second attempt has a 25% chance of success if he fails on the first attempt. What is the minimum number of his attempt to guarantee a goal?
4. যদি n জোড় হয়, তবে T(n) = T(n-1) + 1 এবং n বিদ্যমান হয়, তাহলে T(n) = T(n-2) + 2 । যদি T(1) = 7, তবে T(2020)-এর মান কত?
If n is even, then T(n) = T(n − 1) + 1 and if n is odd then T(n) = T(n − 2) + 2. If T(1) = 7 what is T(2020)?
5. চিত্রে AB এবং AC ব্যাসার্ধ বিশিষ্ট দুটি বৃত্ত যেখানে BC = 65, QR = 33 । যদি CA, B-কেন্দ্র বিশিষ্ট বৃত্তের উপর স্পর্শক হয়, তাহলে AB এর মান কত?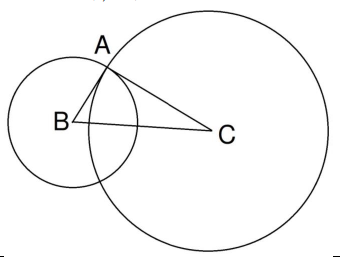
In the figure AB and AC are the radii of the two circles and BC=65. If AC=33 and AC is tangent to the circle with center B,then AC=?
6. সবচেয়ে ছোট ধনাত্মক পূর্ণসংখ্যা নির্ধারণ কর যেটি 2020 দ্বারা নিঃশেষে বিভাজ্য হয়।
Find the smallest positive integer n such that n! is divisible by 2020 without any remainders?.
7.একটি সুসম বহুভুজের অভ্যন্তরীণ কোণ এবং বহিঃস্থ কোণের ব্যবধান 100 ডিগ্রি হলে, সুসম বহুভুজের বাহুর সংখ্যা কত?
If the difference between the measures of an interior angle and an exterior angle of a regular polygon is 100 degrees, how many sides does the polygon have?
8. পাশের চিত্রে ABCD একটি আয়তক্ষেত্র যার AB = 6 এবং BC = 8। BD -কর্ণের উপর X, Y দুটি বিন্দু অবস্থিত এমনভাবে যেন XY = 2 । তাহলে BCY এবং ADX ত্রিভুজগুলির ক্ষেত্রফলের যোগফল \frac{a}{b} যেখানে a এবং b পরস্পর সহমৌলিক এবং ধনাত্মক সংখ্যা। a + b = ?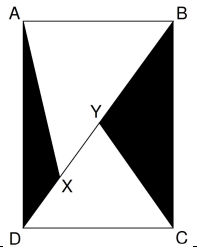
Rectangle ABCD is shown here with AB = 6 and BC = 8. If X and Y lie on diagonal BD, and XY = 2, the total area of shaded triangles BCY and DAX = \frac{a}{b} where a,b are relatively co prime and positve integers. Find a+b.
9. কতগুলো পাঁচ অঙ্কের সংখ্যা আছে যাদের অঙ্কগুলোর গুণফল এবং যোগফল উভয়ই মৌলিক সংখ্যা?
How many numbers are there which contain 5 digits and the sum and product of the digits are both prime numbers?
10. একটা বোর্ডে 1, 2, 3, ………., 12 সংখ্যাগুলো লেখা আছে। প্রতি মিনিটে তুমি এই বোর্ড থেকে চারটা সংখ্যা a, b, c, d বাছাই কর, তাদেরকে মুছে দাও, আর বোর্ডে (a \times a + b \times b + c \times c + d \times d) -এর বর্গমূল লিখে দাও। এভাবে চলতে থাকলে একসময় বোর্ডে আর বাছাই করার মতো চারটা সংখ্যা থাকবে না। সেই সময় বোর্ডে সম্ভাব্য যে সংখ্যাগুলো থাকতে পারে, তাদের মধ্যে সবচেয়ে বড় সংখ্যাটার বর্গের মান কত?
The numbers 1, 2, 3, … , 12 are written on a board. Every minute you choose four numbers a, b, c, d from the board, erase them and write onto the board the square-root of (a×a + b×b + c×c + d×d). If you keep doing this, eventually you won’t have four numbers on the board to choose. When that happens, what is the square of the largest number that can remain on the board?