Class 9 math – ৯ম শ্রেণি গণিত ২য় অধ্যায় অনুশীলনী ২.১ সমাধান
৯ম শ্রেণি গণিত ২য় অধ্যায় অনুশীলনী ২.১ সমাধান, Class 9 Math Chapter 2 Exercise 2.1 Solution, Class 9 Math 2nd Chapter Exercise Solution in Bengali, Ninth Grade Math Chapter 2 Exercise 2.1 Answer in Bangla
প্রশ্ন ১: নিচের সেটগুলোকে তালিকা পদ্ধতিতে প্রকাশ কর
(ক) \{x \in N : x^2 > 9 \text{ এবং } x^3 < 130\}
সমাধান: যে সকল স্বাভাবিক সংখ্যার বর্গ 9 এর চেয়ে বড় এবং ঘন 130 এর চেয়ে ছোট, তাদের নিয়ে সেট তৈরি করতে হবে।
আমরা জানি, স্বাভাবিক সংখ্যার সেট N = \{1, 2, 3, 4, 5, 6, \ldots \}
এখন শর্তগুলো পরীক্ষা করা যাক:
x = 1 হলে, x^2 = 1^2 = 1 < 9 এবং x^3 = 1^3 = 1 < 130 (গ্রহণযোগ্য নয়)
x = 2 হলে, x^2 = 2^2 = 4 < 9 এবং x^3 = 2^3 = 8 < 130 (গ্রহণযোগ্য নয়)
x = 3 হলে, x^2 = 3^2 = 9 = 9 এবং x^3 = 3^3 = 27 < 130 (শর্ত আংশিকভাবে পূর্ণ)
x = 4 হলে, x^2 = 4^2 = 16 > 9 এবং x^3 = 4^3 = 64 < 130 (গ্রহণযোগ্য)
x = 5 হলে, x^2 = 5^2 = 25 > 9 এবং x^3 = 5^3 = 125 < 130 (গ্রহণযোগ্য)
x = 6 হলে, x^2 = 6^2 = 36 > 9 এবং x^3 = 6^3 = 216 > 130 (গ্রহণযোগ্য নয়)
তাহলে, শর্তানুসারে গ্রহণযোগ্য সংখ্যাগুলো হল 4 এবং 5 ।
নির্ণেয় সেট: \{4, 5\}
প্রশ্ন ১: নিচের সেটগুলোকে তালিকা পদ্ধতিতে প্রকাশ কর
(খ) \{x \in Z : x^2 > 5 \text{ এবং } x^2 \leq 36\}
সমাধান: যে সকল পূর্ণসংখ্যার বর্গ 5 এর চেয়ে বড় এবং 36 এর চেয়ে বড় নয়, তাদের নিয়ে সেট তৈরি করতে হবে।
আমরা জানি, পূর্ণসংখ্যার সেট Z = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}
এখন শর্তগুলো পরীক্ষা করা যাক:
x = 0 হলে, x^2 = 0^2 = 0 < 5 (গ্রহণযোগ্য নয়)
x = \pm 1 হলে, x^2 = (\pm 1)^2 = 1 < 5 (গ্রহণযোগ্য নয়)
x = \pm 2 হলে, x^2 = (\pm 2)^2 = 4 < 5 (গ্রহণযোগ্য নয়)
x = \pm 3 হলে, x^2 = (\pm 3)^2 = 9 > 5 এবং 9 < 36 (গ্রহণযোগ্য)
x = \pm 4 হলে, x^2 = (\pm 4)^2 = 16 > 5 এবং 16 < 36 (গ্রহণযোগ্য)
x = \pm 5 হলে, x^2 = (\pm 5)^2 = 25 > 5 এবং 25 < 36 (গ্রহণযোগ্য)
x = \pm 6 হলে, x^2 = (\pm 6)^2 = 36 > 5 এবং 36 = 36 (গ্রহণযোগ্য)
x = \pm 7 হলে, x^2 = (\pm 7)^2 = 49 > 5 এবং 49 > 36 (গ্রহণযোগ্য নয়)
তাহলে, শর্তানুসারে গ্রহণযোগ্য সংখ্যাগুলো হল \pm 3, \pm 4, \pm 5, \pm 6 ।
নির্ণেয় সেট: \{\pm 3, \pm 4, \pm 5, \pm 6\}
প্রশ্ন ১: নিচের সেটগুলোকে তালিকা পদ্ধতিতে প্রকাশ কর**
(গ) \{x \in N : x \text{ হল } 36 \text{ এর গুণনীয়ক এবং } 6 \text{ এর গুণিতক}\}
নবম শ্রেণি গণিত ২য় অধ্যায় সৃজনশীল
সমাধান: যে সকল স্বাভাবিক সংখ্যা 36 এর গুণনীয়ক এবং 6 এর গুণিতক, তাদের নিয়ে সেট তৈরি করতে হবে।
আমরা জানি, স্বাভাবিক সংখ্যা সেট N = \{1, 2, 3, 4, 5, \ldots\}
এখানে, 36 = 1 \times 36 = 2 \times 18 = 3 \times 12 = 4 \times 9 = 6 \times 6
সুতরাং, 36 এর গুণনীয়কসমূহ: 1, 2, 3, 4, 6, 9, 12, 18, 36
এবং 6 এর গুণিতকসমূহ: 6, 12, 18, 24, 30, 36, \ldots
তাহলে, 36 এর গুণনীয়ক এবং 6 এর গুণিতকগুলো হলো যথাক্রমে: 6, 12, 18, 36
নির্ণেয় সেট: \{6, 12, 18, 36\}
প্রশ্ন ১: নিচের সেটগুলোকে তালিকা পদ্ধতিতে প্রকাশ কর
(ঘ) \{x \in N : x^3 > 25 \text{ এবং } x^4 < 264\}
সমাধান: যে সকল স্বাভাবিক সংখ্যার ঘন 25 এর চেয়ে বড় এবং চতুর্ঘাত 264 এর চেয়ে ছোট, তাদের নিয়ে সেট তৈরি করতে হবে।
আমরা জানি, স্বাভাবিক সংখ্যার সেট N = \{1, 2, 3, 4, 5, 6, \ldots\}
এখন শর্তগুলো পরীক্ষা করা যাক:
x = 1 হলে, x^3 = 1^3 = 1 < 25 এবং x^4 = 1^4 = 1 < 264 (গ্রহণযোগ্য নয়)
x = 2 হলে, x^3 = 2^3 = 8 < 25 এবং x^4 = 2^4 = 16 < 264 (গ্রহণযোগ্য নয়)
x = 3 হলে, x^3 = 3^3 = 27 > 25 এবং x^4 = 3^4 = 81 < 264 (গ্রহণযোগ্য)
x = 4 হলে, x^3 = 4^3 = 64 > 25 এবং x^4 = 4^4 = 256 < 264 (গ্রহণযোগ্য)
x = 5 হলে, x^3 = 5^3 = 125 > 25 এবং x^4 = 5^4 = 625 > 264 (গ্রহণযোগ্য নয়)
তাহলে, শর্তানুসারে গ্রহণযোগ্য সংখ্যাগুলো হল 3 এবং 4 ।
নির্ণেয় সেট: \{3, 4\}
প্রশ্ন: নিচের সেটগুলোকে সেট গঠন পদ্ধতিতে প্রকাশ কর
(ক) \{3, 5, 7, 9, 11\}
সমাধান: প্রদত্ত সেটের উপাদানসমূহ হল 3, 5, 7, 9, 11 । এখানে, প্রত্যেকটি উপাদান একটি স্বাভাবিক বিজোড় সংখ্যা যা 1 থেকে বড় এবং 13 থেকে ছোট।
নির্ণেয় সেট: \{x \in N : x \text{ বিজোড় সংখ্যা এবং } 1 < x < 13\}
(খ) \{1, 2, 3, 4, 6, 9, 12, 18, 36\}
সমাধান: প্রদত্ত সেটের উপাদানসমূহ হল 1, 2, 3, 4, 6, 9, 12, 18, 36 । এই সংখ্যাগুলো 36 এর গুণনীয়ক, কারণ তারা প্রত্যেকেই 36 এর বিভাজ্য।
নির্ণেয় সেট: \{x \in N : x \text{ হল } 36 \text{ এর গুণনীয়ক}\}
প্রশ্ন: নিচের সেটগুলোকে সেট গঠন পদ্ধতিতে প্রকাশ কর
(ক) \{1, 2, 3, 4, 6, 9, 12, 18, 36\}
সমাধান: প্রদত্ত সেটের উপাদানসমূহ হল 1, 2, 3, 4, 6, 9, 12, 18, 36 । এখানে, প্রত্যেকটি উপাদান স্বাভাবিক সংখ্যা এবং ৩৬ এর গুণনীয়ক।
নির্ণেয় সেট: \{x \in N : x \text{ হল } 36 \text{ এর গুণনীয়ক}\}
(গ) \{4, 8, 12, 16, 20, 24, 28, 32, 36, 40\}
সমাধান: প্রদত্ত সেটের উপাদানসমূহ হল 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 । এখানে, প্রত্যেকটি উপাদান স্বাভাবিক সংখ্যা এবং এটি 4 এর গুণিতক, যা 40 এর চেয়ে বড় নয়।
নির্ণেয় সেট: \{x \in N : x \text{ হল } 4 \text{ এর গুণিতক এবং } x \leq 40\}
(ঘ) \{\pm 4, \pm 5, \pm 6\}
সমাধান: প্রদত্ত সেটের উপাদানসমূহ হল -6, -5, -4, 4, 5, 6 । এখানে, প্রত্যেকটি উপাদান পূর্ণসংখ্যা এবং তাদের বর্গ 16 এর চেয়ে ছোট নয় এবং ঘন 216 এর চেয়ে বড় নয়।
নির্ণেয় সেট: \{x \in Z : x^2 \geq 16 \text{ এবং } x^3 \leq 216\}
প্রশ্ন ৩: যদি A = \{2, 3, 4\} , B = \{1, 2, a\} এবং C = \{2, a, b\} হয়, তবে নিচের সেটগুলো নির্ণয় কর:
(ক) B \setminus C
সমাধান: দেওয়া আছে, B = \{1, 2, a\} এবং C = \{2, a, b\} ।
সুতরাং, B \setminus C = \{1, 2, a\} \setminus \{2, a, b\} = \{1\} (উত্তর)
(খ) A \cup B
সমাধান: দেওয়া আছে, A = \{2, 3, 4\} এবং B = \{1, 2, a\} ।
সুতরাং, A \cup B = \{2, 3, 4\} \cup \{1, 2, a\} = \{1, 2, 3, 4, a\} (উত্তর)
(গ) A \cap C
সমাধান: দেওয়া আছে, A = \{2, 3, 4\} এবং C = \{2, a, b\} ।
সুতরাং, A \cap C = \{2, 3, 4\} \cap \{2, a, b\} = \{2\} (উত্তর)
প্রশ্ন ৩: যদি A = \{2, 3, 4\} , B = \{1, 2, a\} এবং C = \{2, a, b\} হয়, তবে নিচের সেটগুলো নির্ণয় কর:
(ঘ) A \cup (B \cap C)
সমাধান: দেওয়া আছে, A = \{2, 3, 4\} , B = \{1, 2, a\} এবং C = \{2, a, b\} ।
প্রথমে, B \cap C = \{1, 2, a\} \cap \{2, a, b\} = \{2, a\}
সুতরাং, A \cup (B \cap C) = \{2, 3, 4\} \cup \{2, a\} = \{2, 3, 4, a\} (উত্তর)
(ঙ) A \cap (B \cup C)
সমাধান: দেওয়া আছে, A = \{2, 3, 4\} , B = \{1, 2, a\} এবং C = \{2, a, b\} ।
প্রথমে, B \cup C = \{1, 2, a\} \cup \{2, a, b\} = \{1, 2, a, b\}
সুতরাং, A \cap (B \cup C) = \{2, 3, 4\} \cap \{1, 2, a, b\} = \{2\} (উত্তর)
প্রশ্ন ৪: যদি U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} , B = \{2, 4, 6\} এবং C = \{3, 4, 5, 6, 7\} হয়, তবে নিম্নলিখিত ক্ষেত্রে সত্যতা যাচাই কর:
(i) (A \cup B)' = A' \cap B'
সমাধান: দেওয়া আছে, U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} এবং B = \{2, 4, 6\} ।
প্রথমে, A \cup B = \{1, 3, 5\} \cup \{2, 4, 6\} = \{1, 2, 3, 4, 5, 6\}
তাহলে, বামপক্ষ (A \cup B)' = U \setminus (A \cup B) = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{1, 2, 3, 4, 5, 6\} = \{7\}
এখন, A' = U \setminus A = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{1, 3, 5\} = \{2, 4, 6, 7\}
এবং B' = U \setminus B = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{2, 4, 6\} = \{1, 3, 5, 7\}
সুতরাং, ডানপক্ষ A' \cap B' = \{2, 4, 6, 7\} \cap \{1, 3, 5, 7\} = \{7\}
অর্থাৎ, (A \cup B)' = A' \cap B' (সত্যতা যাচাই করা হলো)।
প্রশ্ন ৪: যদি U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} , B = \{2, 4, 6\} এবং C = \{3, 4, 5, 6, 7\} হয়, তবে নিম্নলিখিত ক্ষেত্রে সত্যতা যাচাই কর:
(ii) (B \cap C)' = B' \cup C'
সমাধান: দেওয়া আছে, U = \{1, 2, 3, 4, 5, 6, 7\} , B = \{2, 4, 6\} এবং C = \{3, 4, 5, 6, 7\} ।
প্রথমে, B \cap C = \{2, 4, 6\} \cap \{3, 4, 5, 6, 7\} = \{4, 6\}
তাহলে, বামপক্ষ (B \cap C)' = U \setminus (B \cap C) = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{4, 6\} = \{1, 2, 3, 5, 7\}
এখন, B' = U \setminus B = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{2, 4, 6\} = \{1, 3, 5, 7\}
এবং C' = U \setminus C = \{1, 2, 3, 4, 5, 6, 7\} \setminus \{3, 4, 5, 6, 7\} = \{1, 2\}
সুতরাং, ডানপক্ষ B' \cup C' = \{1, 3, 5, 7\} \cup \{1, 2\} = \{1, 2, 3, 5, 7\}
তাহলে, (B \cap C)' = B' \cup C' (সত্যতা যাচাই করা হলো)।
(iii) (A \cup B) \cap C = (A \cap C) \cup (B \cap C)
সমাধান:দেওয়া আছে, U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} , B = \{2, 4, 6\} এবং C = \{3, 4, 5, 6, 7\} ।
প্রথমে, A \cup B = \{1, 3, 5\} \cup \{2, 4, 6\} = \{1, 2, 3, 4, 5, 6\}
তাহলে, বামপক্ষ (A \cup B) \cap C = \{1, 2, 3, 4, 5, 6\} \cap \{3, 4, 5, 6, 7\} = \{3, 4, 5, 6\}
এখন, A \cap C = \{1, 3, 5\} \cap \{3, 4, 5, 6, 7\} = \{3, 5\}
এবং B \cap C = \{2, 4, 6\} \cap \{3, 4, 5, 6, 7\} = \{4, 6\}
সুতরাং, ডানপক্ষ (A \cap C) \cup (B \cap C) = \{3, 5\} \cup \{4, 6\} = \{3, 4, 5, 6\}
তাহলে, (A \cup B) \cap C = (A \cap C) \cup (B \cap C) (সত্যতা যাচাই করা হলো)।
প্রশ্ন ৪: যদি U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} , B = \{2, 4, 6\} এবং C = \{3, 4, 5, 6, 7\} হয়, তবে নিম্নলিখিত ক্ষেত্রে সত্যতা যাচাই কর:
(iv) (A \cap B) \cup C = (A \cup C) \cap (B \cup C)
সমাধান:দেওয়া আছে, U = \{1, 2, 3, 4, 5, 6, 7\} , A = \{1, 3, 5\} , B = \{2, 4, 6\} , এবং C = \{3, 4, 5, 6, 7\} ।
প্রথমে, A \cap B = \{1, 3, 5\} \cap \{2, 4, 6\} = \{\} (খালি সেট)
তাহলে, বামপক্ষ (A \cap B) \cup C = \{\} \cup \{3, 4, 5, 6, 7\} = \{3, 4, 5, 6, 7\}
এখন, A \cup C = \{1, 3, 5\} \cup \{3, 4, 5, 6, 7\} = \{1, 3, 4, 5, 6, 7\}
এবং B \cup C = \{2, 4, 6\} \cup \{3, 4, 5, 6, 7\} = \{2, 3, 4, 5, 6, 7\}
সুতরাং, ডানপক্ষ (A \cup C) \cap (B \cup C) = \{1, 3, 4, 5, 6, 7\} \cap \{2, 3, 4, 5, 6, 7\} = \{3, 4, 5, 6, 7\}
অতএব, (A \cap B) \cup C = (A \cup C) \cap (B \cup C) (সত্যতা যাচাই করা হলো)।
প্রশ্ন ৫: যদি Q = \{x, y\} এবং R = \{m, n, l\} হয়, তবে P(Q) এবং P(R) নির্ণয় কর।
সমাধান:
দেওয়া আছে, Q = \{x, y\} এবং R = \{m, n, l\} ।
Q সেটের উপসেটগুলো হলো: \{x, y\}, \{x\}, \{y\}, \emptyset
সুতরাং, P(Q) = \{\{x, y\}, \{x\}, \{y\}, \emptyset\} (উত্তর)
R সেটের উপসেটগুলো হলো: \{m, n, l\}, \{m, n\}, \{m, l\}, \{n, l\}, \{m\}, \{n\}, \{l\}, \emptyset
সুতরাং, P(R) = \{\{m, n, l\}, \{m, n\}, \{m, l\}, \{n, l\}, \{m\}, \{n\}, \{l\}, \emptyset\} (উত্তর)
প্রশ্ন ৬:যদি A = {a, b}, B = {a, b, c} এবং C = A ∪ B হলে, দেখাও যে, P(C) এর উপাদান সংখ্যা 2^n, যেখানে n হচ্ছে C এর উপাদান সংখ্যা।
সমাধানদেওয়া আছে, A = {a, b}, B = {a, b, c} এবং C = A ∪ B
তাহলে, C = A ∪ B = {a, b} ∪ {a, b, c} = {a, b, c}
এখন, C সেটের উপসেটগুলো হলো {a, b, c}, {a, b}, {b, c}, {a, c}, {a}, {b}, {c}, ∅
সুতরাং, P(C) = {{a, b, c}, {a, b}, {b, c}, {a, c}, {a}, {b}, {c}, ∅}
তাহলে, P(C) এর উপাদান সংখ্যা = 8 = 2^3
অতএব, C সেটের উপাদান সংখ্যা n হলে P(C) সেটের উপাদান সংখ্যা 2^n। (দেখানো হলো)
প্রশ্ন ৭: (ক) (x – 1, y + 2) = (y – 2, 2x + 1) হলে, x এবং y এর মান নির্ণয় কর।
সমাধান: দেওয়া আছে, (x – 1, y + 2) = (y – 2, 2x + 1)
ক্রমজোড়ের সংজ্ঞানুসারে, x – 1 = y – 2 —————————– (i)
এবং y + 2 = 2x + 1 ———————————– (ii)
সমীকরণ (i) হতে পাই, x – 1 = y – 2
অথবা, x = y – 2 + 1
সুতরাং, x = y – 1 ————————- (iii)
সমীকরণ (ii)-এ x এর মান বসিয়ে পাই,
y + 2 = 2(y – 1) + 1
অথবা, y + 2 = 2y – 2 + 1
অথবা, y – 2y = -2 + 1 – 2
অথবা, -y = -3
সুতরাং, y = 3
এখন, সমীকরণ (iii) এ y এর মান বসিয়ে পাই,
x = 3 – 1 সুতরাং, x = 2
নির্ণেয় মান x = 2, y = 3
দুঃখিত, আমি তোমার নির্দেশনা ঠিকমতো অনুসরণ করতে পারিনি। এবার গাণিতিক বাক্যের প্রথমে এবং শেষে যোগ করছি:
(খ) (ax - cy, a^2 - c^2) = (0, ay - cx) হলে, (x, y) এর মান নির্ণয় কর।
সমাধান : দেওয়া আছে, (ax - cy, a^2 - c^2) = (0, ay - cx)
ক্রমজোড়ের সংজ্ঞানুসারে, ax - cy = 0 —————————- (i)
এবং a^2 - c^2 = ay - cx
অথবা, -cx + ay = a^2 - c^2 ———————–(ii)
সমীকরণ (i) হতে পাই, ax - cy = 0
বা, ax = cy
অতএব, x = \frac{cy}{a} ————————(iii)
সমীকরণ (ii) এ x এর মান বসিয়ে পাই,
-c \cdot \frac{cy}{a} + ay = a^2 - c^2
অথবা, \frac{-c^2y + a^2y}{a} = a^2 - c^2
অথবা, \frac{y(a^2 - c^2)}{a} = a^2 - c^2
অথবা, y(a^2 - c^2) = a(a^2 - c^2)
অতএব, y = a [উভয় পক্ষকে a^2 - c^2 দ্বারা ভাগ করে]
এখন, সমীকরণ (iii) এ y এর মান বসিয়ে পাই,
x = \frac{c \cdot a}{a}
অতএব, x = c
নির্ণেয় মান (x, y) = (c, a)
(গ) (6x - y, 13) = (1, 3x + 2y) হলে, (x, y) নির্ণয় কর।
সমাধান : দেওয়া আছে, (6x - y, 13) = (1, 3x + 2y)
ক্রমজোড়ের সংজ্ঞানুসারে, 6x - y = 1 ————————- (i)
এবং 13 = 3x + 2y
অথবা, 3x + 2y = 13 —————————(ii)
সমীকরণ (i) কে 2 দ্বারা গুণ করে (ii) নং সমীকরণের সাথে যোগ করি,
12x - 2y = 2
3x + 2y = 13
(+ করে) 15x = 15
অতএব, x = 1
সমীকরণ (ii) এ x এর মান বসিয়ে পাই, 3 \times 1 + 2y = 13
বা, 3 + 2y = 13
বা, 2y = 13 - 3
বা, 2y = 10
বা, y = \frac{10}{2}
অতএব, y = 5
নির্ণেয় মান (x, y) = (1, 5)
(ক) P = {a}, Q = {b, c} হলে, P × Q এবং Q × P নির্ণয় কর।
সমাধান : দেওয়া আছে, P = {a} এবং Q = {b, c}
∴ P × Q = {a} × {b, c} = {(a, b), (a, c)}
এবং Q × P = {b, c} × {a} = {(b, a), (c, a)}
(খ) A = {3, 4, 5}, B = {4, 5, 6} এবং C = {x, y} হলে, (A ∩ B) × C নির্ণয় কর।
সমাধান : দেওয়া আছে, A = {3, 4, 5}, B = {4, 5, 6} এবং C = {x, y}
এখন, A ∩ B = {3, 4, 5} ∩ {4, 5, 6} = {4, 5}
∴ (A ∩ B) × C = {4, 5} × {x, y}
= {(4, x), (4, y), (5, x), (5, y)}
(গ) P = {3, 5, 7}, Q = {5, 7} এবং R = P \ Q হলে, (P ∪ Q) × R নির্ণয় কর।
সমাধান : দেওয়া আছে, P = {3, 5, 7}, Q = {5, 7}
∴ R = P \ Q = {3, 5, 7} \ {5, 7} = {3}
এখন, P ∪ Q = {3, 5, 7} ∪ {5, 7} = {3, 5, 7}
∴ (P ∪ Q) × R = {3, 5, 7} × {3} = {(3, 3), (5, 3), (7, 3)}
প্রশ্ন ৯: A ও B যথাক্রমে 35 এবং 45 এর সকল গুণনীয়কের সেট হলে, A ∪ B এবং A ∩ B নির্ণয় কর।
সমাধান : এখানে, 35 = 1 × 35 = 5 × 7
35 এর গুণনীয়কগুলো হলো 1, 5, 7, 35
∴ A = {1, 5, 7, 35}
এবং 45 = 1 × 45 = 3 × 15 = 5 × 9
45 এর গুণনীয়কগুলো হলো, 1, 3, 5, 9, 15, 45
∴ B = {1, 3, 5, 9, 15, 45}
∴ A ∪ B = {1, 5, 7, 35} ∪ {1, 3, 5, 9, 15, 45}
= {1, 3, 5, 7, 9, 15, 35, 45}
এবং A ∩ B = {1, 5, 7, 35} ∩ {1, 3, 5, 9, 15, 45}
= {1, 5}
প্রশ্ন ১০: যে সকল স্বাভাবিক সংখ্যা দ্বারা 346 এবং 556 কে ভাগ করলে প্রতিক্ষেত্রে 31 অবশিষ্ট থাকে, এদের সেট নির্ণয় কর।
সমাধান : যে স্বাভাবিক সংখ্যা দ্বারা 346 এবং 556 কে ভাগ করলে প্রতিক্ষেত্রে 31 অবশিষ্ট থাকে, সে সংখ্যা হবে 31 অপেক্ষা বড় এবং 346 – 31 = 315 এবং 556 – 31 = 525 এর সাধারণ গুণনীয়ক।
মনে করি, 31 অপেক্ষা বড় 315 এর গুণনীয়কের সেট A এবং 525 এর গুণনীয়কের সেট B
এখানে, 315 = 1 × 315 = 3 × 105 = 5 × 63 = 7 × 45 = 9 × 35 = 15 × 21
31 অপেক্ষা বড় 315 এর গুণনীয়কগুলো হলো যথাক্রমে 35, 45, 63, 105, 315
∴ A = {35, 45, 63, 105, 315}
আবার, 525 = 1 × 525 = 3 × 175 = 5 × 105 = 7 × 75 = 15 × 35 = 21 × 25
31 অপেক্ষা বড় 525 এর গুণনীয়কগুলো হলো যথাক্রমে 35, 75, 105, 175, 525
∴ B = {35, 75, 105, 175, 525}
∴ A ∩ B = {35, 45, 63, 105, 315} ∩ {35, 75, 105, 175, 525}
= {35, 105}
নির্ণেয় সেট {35, 105}
প্রশ্ন ১১: কোনো শ্রেণির 30 জন শিক্ষার্থীর মধ্যে 20 জন ফুটবল এবং 15 জন ক্রিকেট খেলা পছন্দ করে। দুইটি খেলাই পছন্দ করে এমন শিক্ষার্থীর সংখ্যা 10; কতজন শিক্ষার্থী দুইটি খেলাই পছন্দ করে না তা ভেন চিত্রের সাহায্যে নির্ণয় কর।
সমাধান : নিচের আয়তাকার ভেন চিত্রটি 30 জন শিক্ষার্থীর সেট S নির্দেশ করে F ও C দ্বারা নির্দেশিত বৃত্তাকার ক্ষেত্র দুইটি যথাক্রমে ফুটবল এবং ক্রিকেট খেলা পছন্দ করে এমন শিক্ষার্থীর সেট নির্দেশ করে। ভেন চিত্রটি চারটি নিশ্চেদ সেটে বিভক্ত হয়েছে, যাদের P1, P2, P3, ও P4 দ্বারা বিভক্ত করা হলো।
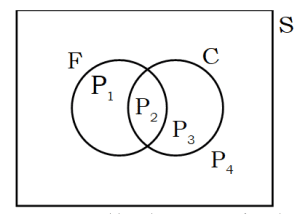
এখানে, P2 = F ∩ C = দুইটি খেলাই পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 10
P1 = F \ P2 = শুধু ফুটবল খেলা পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 20 – 10 = 10
P3 = C \ P2 = শুধু ক্রিকেট খেলা পছন্দ করে শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 15 – 10 = 5
∴ F ∪ C = P1 ∪ P2 ∪ P3 = এক এবং উভয় খেলা পছন্দ শিক্ষার্থীদের সেট এবং সদস্য সংখ্যা = 10 + 10 + 5 = 25
∴ P4 = S \ (F ∪ C) = দুইটি খেলাই পছন্দ করে না শিক্ষার্থীদের সেট এবং এর সদস্য সংখ্যা = 30 – 25 = 5
নির্ণেয় 5 জন শিক্ষার্থী দুইটি খেলাই পছন্দ করে না
প্রশ্ন ১২: ১০০ জন শিক্ষার্থীর মধ্যে কোনো পরীক্ষায় 65% শিক্ষার্থী বাংলায়, 48% শিক্ষার্থী বাংলা ও ইংরেজি উভয় বিষয়ে পাস এবং 15% শিক্ষার্থী উভয় বিষয়ে ফেল করেছে।
ক. সংক্ষিপ্ত বিবরণসহ ওপরের তথ্যগুলো ভেন চিত্রে প্রকাশ কর
খ. শুধু বাংলায় ও ইংরেজিতে পাস করেছে তাদের সংখ্যা নির্ণয় কর
গ. উভয় বিষয়ে পাস এবং উভয় বিষয়ে ফেল সংখ্যাদ্বয়ের মৌলিক গুণনীয়কসমূহের সেট দুইটির সংযোগ সেট নির্ণয় কর
সমাধান :
(ক) ভেন চিত্রে আয়তাকার ক্ষেত্রটি 100 জন পরীক্ষার্থীর সেট U এবং পরস্পরচ্ছেদী দুইটি বৃত্তক্ষেত্র দ্বারা বাংলা ও ইংরেজিতে পাস পরীক্ষার্থীদের সেট যথাক্রমে B ও F নির্দেশ করা হলো।

(খ) এখানে, Q = B ∩ E = উভয় বিষয়ে পাস পরীক্ষার্থীদের সেট, যার সদস্য সংখ্যা 48
∴ P = শুধু বাংলায় পাস পরীক্ষার্থীদের সেট, যার সদস্য সংখ্যা 65 – 48 = 17 এবং R = শুধু ইংরেজিতে পাস পরীক্ষার্থীদের সেট যার সদস্য সংখ্যা = 100 – (17 + 48 + 15) = 20
(গ) উভয় বিষয়ে পাস করা শিক্ষার্থীর সংখ্যা = 48
এবং উভয় বিষয়ে ফেল করা শিক্ষার্থীর সংখ্যা = 15
ধরি, 48 এর মৌলিক গুণনীয়ক সমূহের সেট A এবং 15 এর মৌলিক গুণনীয়কসমূহের সেট B
48 এর মৌলিক গুণনীয়ক গুলো হলো 2, 3 এবং 15 এর মৌলিক গুণনীয়ক হলো 3, 5
∴ A = {2, 3} এবং B = {3, 5}
∴ A ∪ B = {2, 3} ∪ {3, 5} = {2, 3, 5}
